40 Is What Percent Of 24
Kalali
Apr 13, 2025 · 5 min read
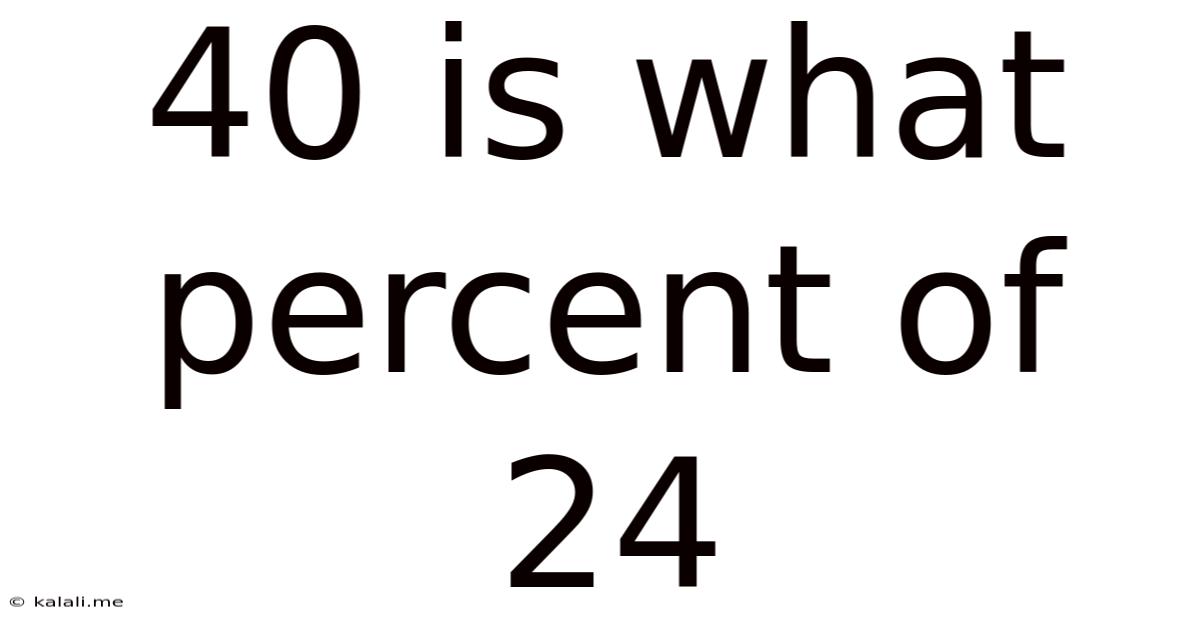
Table of Contents
40 is What Percent of 24? Understanding Percentages and Real-World Applications
This seemingly simple question, "40 is what percent of 24?", unlocks a fundamental concept in mathematics with far-reaching applications in everyday life. Understanding how to calculate percentages is crucial for everything from calculating discounts and taxes to analyzing financial data and understanding statistics. This article will not only answer the question directly but also delve into the underlying principles, explore different methods of calculation, and demonstrate the practical relevance of percentage calculations.
Meta Description: Learn how to calculate percentages, specifically solving "40 is what percent of 24?". This guide covers various methods, real-world applications, and practical tips for mastering percentage calculations.
Understanding the Fundamentals of Percentages
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this basic definition is key to solving percentage problems.
To represent a percentage, we use the "%" symbol. This symbol is a shorthand way of expressing the fraction's denominator as 100. For example, 25% can be written as 25/100, 0.25, or one-quarter. These are all equivalent representations of the same value.
Method 1: Using the Percentage Formula
The most straightforward way to solve "40 is what percent of 24?" is using the standard percentage formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 40 (the number we're considering as a part of the whole)
- Whole: 24 (the total number, the whole amount)
Plugging the values into the formula:
(40 / 24) * 100 = 166.67%
Therefore, 40 is 166.67% of 24. This result indicates that 40 is significantly larger than 24.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
40 / 24 = x / 100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
40 * 100 = 24 * x
4000 = 24x
x = 4000 / 24
x = 166.67%
This method confirms the result obtained using the percentage formula.
Method 3: Using Decimal Conversion
We can also solve this problem by first converting the fraction 40/24 into a decimal and then multiplying by 100 to express it as a percentage.
40 / 24 ≈ 1.6667
1.6667 * 100 = 166.67%
This approach provides the same answer and demonstrates the interchangeability between fractions, decimals, and percentages.
Understanding the Result: Percentages Greater Than 100%
The result, 166.67%, might seem unusual at first. Percentages are often associated with values between 0% and 100%. However, percentages greater than 100% simply indicate that the "part" is larger than the "whole." In this context, 40 is more than 24, hence the percentage exceeds 100%. This concept is common in scenarios involving growth, increase, or comparing values where one significantly surpasses the other. For instance, if a company's profits this year are 150% of last year's profits, it means this year's profits are 1.5 times larger than last year's.
Real-World Applications of Percentage Calculations
Percentage calculations are incredibly versatile and applicable across diverse fields:
- Finance: Calculating interest rates, loan repayments, returns on investment, profit margins, and tax rates.
- Retail: Determining discounts, sales tax, and final prices after applying markups or reductions.
- Science: Representing experimental data, analyzing statistical significance, and expressing concentrations (e.g., percentage composition of a chemical compound).
- Data Analysis: Expressing changes in data over time (e.g., percentage increase or decrease in sales), calculating statistical measures (e.g., percentages in survey responses), and visualizing data using charts and graphs.
- Everyday Life: Calculating tips at restaurants, determining the percentage of ingredients in recipes, understanding nutritional information, and interpreting statistics in news reports.
Practical Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice solving percentage problems, the more comfortable and proficient you'll become. Start with simple problems and gradually increase the complexity.
- Use Different Methods: Familiarize yourself with various methods of calculating percentages (formula, proportion, decimal conversion) to choose the approach that best suits each specific problem.
- Understand the Context: Pay close attention to the context of the problem to correctly identify the "part" and the "whole." Misinterpreting these values will lead to an incorrect result.
- Utilize Calculators and Software: While manual calculation is important for understanding the underlying principles, don't hesitate to use calculators or spreadsheet software (like Excel or Google Sheets) to efficiently solve complex percentage problems. These tools can handle large numbers and intricate calculations quickly and accurately.
- Check Your Work: Always double-check your answers, especially when dealing with important financial or scientific calculations. A simple error in calculation can have significant consequences.
Beyond the Basics: More Complex Percentage Problems
While "40 is what percent of 24?" is a foundational percentage problem, the concept extends to more complex scenarios. These might involve multiple percentage changes, percentage increases or decreases over time, or calculating percentages within larger datasets. Understanding the fundamentals laid out in this article will provide a strong base for tackling these more advanced problems.
Conclusion: The Importance of Percentage Literacy
Proficiency in percentage calculations is a fundamental skill with broad applications across numerous aspects of life. Mastering this skill empowers individuals to make informed decisions in financial matters, interpret data effectively, and confidently navigate various situations where percentage calculations are essential. By understanding the principles, methods, and applications discussed in this article, you can develop a strong foundation for handling percentages with ease and accuracy. Remember to practice regularly, utilize available tools, and always double-check your results to ensure you are working with accurate and reliable information.
Latest Posts
Latest Posts
-
Is An Egg A Fruit Or Vegetable
Jul 05, 2025
-
How Many Cups In A Bag Of Chocolate Chips
Jul 05, 2025
-
Spyware Can Result In All Of The Following Except
Jul 05, 2025
-
What Year Were 16 Year Olds Born
Jul 05, 2025
-
Two Letter Symbol From The Periodic Table
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about 40 Is What Percent Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.