41 Out Of 50 As A Percentage
Kalali
Mar 09, 2025 · 5 min read
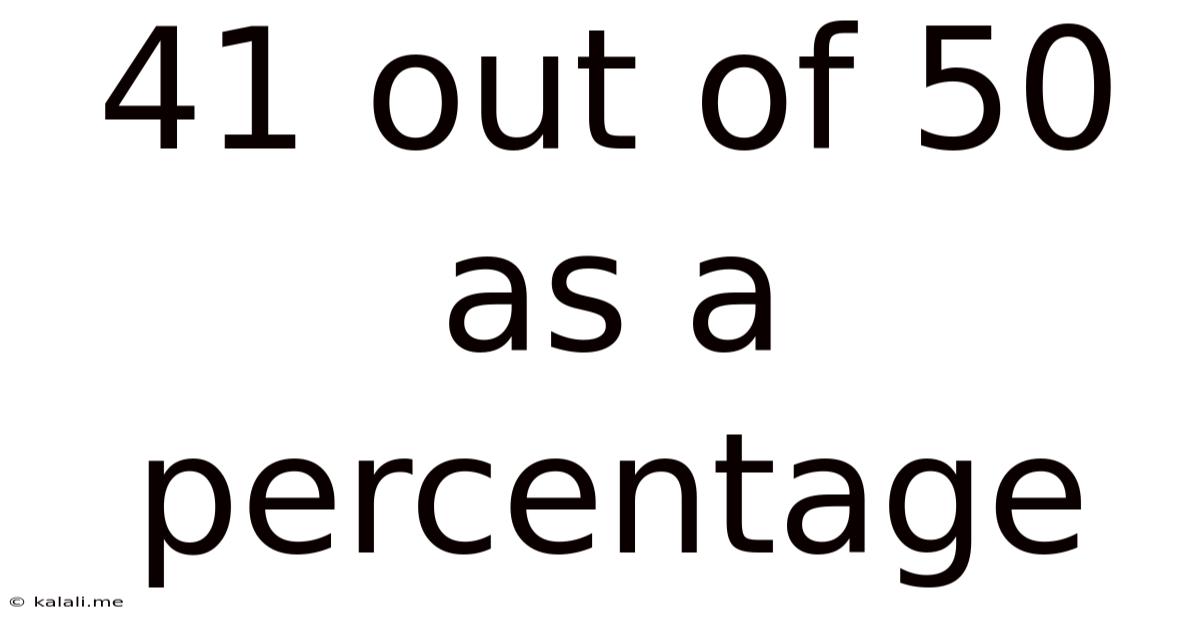
Table of Contents
41 out of 50 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis. Understanding how to convert fractions into percentages is crucial for interpreting data and making informed decisions. This comprehensive guide delves into the calculation of 41 out of 50 as a percentage, exploring various methods and providing practical applications. We'll also touch upon related percentage calculations and offer tips for improving your percentage calculation skills.
Understanding Percentages
Before we dive into the specific calculation, let's establish a clear understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a proportion or ratio out of a total of 100.
For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or 0.5 as a decimal. Percentages are used extensively to represent proportions, rates, and changes in various contexts.
Calculating 41 out of 50 as a Percentage: Method 1 - The Fraction Method
The most straightforward way to calculate 41 out of 50 as a percentage involves expressing the given numbers as a fraction and then converting it to a percentage.
-
Express as a Fraction: The phrase "41 out of 50" can be written as the fraction 41/50.
-
Convert to Decimal: To convert the fraction to a decimal, divide the numerator (41) by the denominator (50): 41 ÷ 50 = 0.82
-
Convert to Percentage: To express the decimal as a percentage, multiply it by 100: 0.82 × 100 = 82%
Therefore, 41 out of 50 is equal to 82%.
Calculating 41 out of 50 as a Percentage: Method 2 - The Proportion Method
This method utilizes the concept of proportions to solve the problem. We set up a proportion where x represents the percentage we want to find:
41/50 = x/100
To solve for x, we cross-multiply:
50x = 4100
Then, divide both sides by 50:
x = 4100 ÷ 50 = 82
Therefore, x = 82%, confirming our previous result. This method provides a more algebraic approach to percentage calculations.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in various real-world scenarios. Here are some examples:
-
Academic Performance: Students frequently encounter percentage calculations to determine their grades based on marks obtained in exams or assignments. For example, if a student scores 41 out of 50 on a test, their percentage score is 82%, indicating a strong performance.
-
Financial Calculations: Percentages are crucial in finance, used to calculate interest rates, discounts, taxes, and profit margins. Understanding percentage changes helps in analyzing investment performance and making informed financial decisions. For example, a 5% increase in a stock's price signifies growth.
-
Statistical Analysis: Percentages are widely used in statistical analysis to represent proportions within datasets. They're essential for interpreting survey results, market research data, and demographic information. For instance, 82% of respondents might indicate preference for a particular product.
-
Sales and Marketing: Businesses use percentages to track sales performance, calculate discounts, and analyze market share. Discounts like "20% off" are common examples of percentage applications in marketing.
Beyond 41 out of 50: Mastering Percentage Calculations
While understanding how to calculate 41 out of 50 is important, mastering percentage calculations involves handling various scenarios. Let's explore some related calculations:
-
Calculating the Percentage Increase or Decrease: This involves determining the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] × 100. For example, if a price increases from $50 to $61, the percentage increase is [(61-50)/50] × 100 = 22%.
-
Finding a Percentage of a Number: This is often required to calculate discounts or commissions. To find X% of a number Y, you multiply Y by (X/100). For example, to find 20% of $100, you calculate 100 × (20/100) = $20.
-
Calculating the Original Value: If you know the final value and the percentage increase or decrease, you can calculate the original value using algebraic manipulation.
-
Working with Complex Percentages: Sometimes, you might need to work with multiple percentages sequentially, such as calculating compound interest. Understanding the order of operations is critical in such cases.
Tips for Improving Percentage Calculation Skills
-
Practice Regularly: Consistent practice is key to mastering percentage calculations. Solve a variety of problems to build your confidence and familiarity with different methods.
-
Use Visual Aids: Diagrams, charts, and graphs can make it easier to understand and visualize percentage relationships.
-
Utilize Online Calculators: While understanding the underlying principles is crucial, online calculators can help check your answers and save time on complex calculations.
-
Break Down Complex Problems: If you encounter a complex percentage problem, break it down into smaller, manageable steps.
-
Understand the Underlying Concepts: A strong grasp of fractions, decimals, and proportions is essential for accurate and efficient percentage calculations.
Conclusion
Calculating 41 out of 50 as a percentage, resulting in 82%, is a fundamental percentage calculation. This guide has explored two methods for solving this problem: the fraction method and the proportion method. Beyond this specific example, mastering percentage calculations requires understanding various related concepts, including percentage increase/decrease, finding a percentage of a number, and working with complex percentage scenarios. By practicing regularly and utilizing various resources, you can significantly improve your ability to solve percentage problems and apply them effectively in various real-world situations. The ability to confidently handle percentage calculations is a valuable skill that enhances decision-making in academic, financial, and professional contexts.
Latest Posts
Latest Posts
-
What Is The Shortest Chapter In The Bible
Jul 02, 2025
-
What Has 4 Letters Sometimes Has 9
Jul 02, 2025
-
How Many Milliliters In A Half Gallon
Jul 02, 2025
-
How Much Can I Sell Bro For
Jul 02, 2025
-
How Many Bottles Is 64 Oz Of Water
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about 41 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.