45 Is What Percent Of 60
Kalali
Apr 16, 2025 · 5 min read
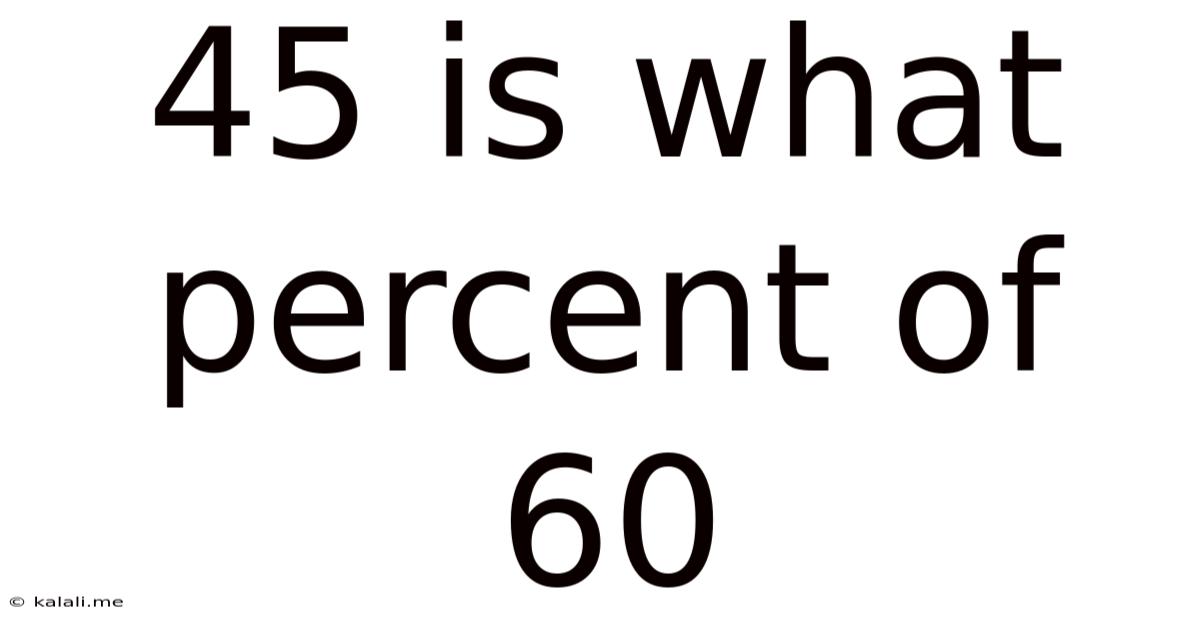
Table of Contents
45 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "45 is what percent of 60?", opens the door to a world of percentage calculations crucial for various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. This comprehensive guide will not only answer this specific question but also equip you with the knowledge and skills to tackle any percentage problem with confidence. We'll explore multiple methods for solving this type of problem, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Meta Description: Learn how to calculate percentages with this in-depth guide. We'll solve the problem "45 is what percent of 60?" using multiple methods, exploring the fundamental concepts and offering practical applications. Master percentage calculations for everyday use and beyond.
Understanding Percentages: The Basics
Before diving into the solution, let's establish a solid foundation in percentage concepts. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." So, 50% means 50 out of 100, which is equivalent to ½ or 0.5 as a decimal. Understanding this fundamental relationship is key to mastering percentage calculations.
Percentage problems often involve three key elements:
- The Part: The portion of the whole we're interested in. In our example, the part is 45.
- The Whole: The total amount or the complete quantity. In our example, the whole is 60.
- The Percentage: The ratio of the part to the whole, expressed as a percentage. This is what we need to find.
Method 1: Using the Percentage Formula
The most direct way to solve "45 is what percent of 60?" is by using the basic percentage formula:
(Part / Whole) x 100% = Percentage
Let's substitute the values from our problem:
(45 / 60) x 100% = Percentage
-
Divide the Part by the Whole: 45 divided by 60 equals 0.75.
-
Multiply by 100%: 0.75 multiplied by 100% equals 75%.
Therefore, 45 is 75% of 60.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent our problem as:
45/60 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
45 * 100 = 60 * x
4500 = 60x
Now, divide both sides by 60:
x = 4500 / 60
x = 75
Therefore, 45 is 75% of 60.
Method 3: Using Decimal Equivalents
We can also solve this using decimal equivalents. First, express the fraction as a decimal:
45/60 = 0.75
Then, convert the decimal to a percentage by multiplying by 100%:
0.75 * 100% = 75%
This method is particularly useful when dealing with simpler fractions or when using a calculator.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in many real-life scenarios. Here are some examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $100, you can calculate the discount amount and the final price using percentage calculations.
-
Determining Tax Amounts: Calculating sales tax or income tax involves determining a percentage of a total amount.
-
Analyzing Financial Statements: Investors and financial analysts use percentage calculations to analyze financial reports, such as profit margins, return on investment (ROI), and growth rates.
-
Understanding Statistics: Percentages are frequently used in statistics to represent proportions and probabilities.
-
Everyday Budgeting: Tracking expenses and income often involves working with percentages to understand spending habits and financial health.
Advanced Percentage Problems and Calculations
While the problem "45 is what percent of 60?" is relatively straightforward, understanding percentage calculations extends to more complex scenarios. Let's explore some variations:
-
Finding the Whole: If you know the part and the percentage, you can calculate the whole. For instance, if 25% of a number is 10, what is the number? This can be solved using the formula: Whole = (Part / Percentage) x 100.
-
Finding the Part: If you know the whole and the percentage, you can calculate the part. For example, what is 15% of 200? This is solved by multiplying the whole by the percentage (200 * 0.15 = 30).
-
Percentage Change: Calculating percentage change (increase or decrease) is crucial in various applications. The formula for percentage change is: [(New Value - Old Value) / Old Value] x 100%. This is used to track changes in prices, populations, or any other quantifiable data.
-
Compound Interest: Compound interest calculations involve applying percentage increases repeatedly over time. Understanding compound interest is crucial for managing investments and loans.
Tips and Tricks for Mastering Percentage Calculations
Here are some valuable tips to help you improve your proficiency in percentage calculations:
-
Practice Regularly: The more you practice, the more comfortable you'll become with different types of percentage problems.
-
Use a Calculator: While mental calculations are helpful, using a calculator can save time and ensure accuracy, particularly for complex problems.
-
Visualize the Problem: Try to visualize the problem using diagrams or charts to enhance understanding.
-
Break Down Complex Problems: If you encounter a complex problem, break it down into smaller, more manageable parts.
-
Check Your Answers: Always double-check your answers to ensure accuracy.
Conclusion: Mastering the World of Percentages
The question "45 is what percent of 60?" might seem simple at first glance, but it provides a springboard to understanding the vast applications of percentage calculations in various aspects of life. By mastering the fundamental concepts and utilizing the various methods outlined in this guide, you'll develop a strong foundation for tackling any percentage problem, empowering you to make informed decisions in your personal and professional life. Remember to practice consistently, explore different problem types, and use the available tools to enhance your understanding and improve your skills. With dedication and practice, you'll become proficient in the world of percentages and harness its power for practical applications.
Latest Posts
Latest Posts
-
How Many Hours Is 285 Minutes
Apr 19, 2025
-
How Many Species Of Reptiles Are There
Apr 19, 2025
-
6 Cups Equals How Many Pints
Apr 19, 2025
-
How To Do Mole To Mass Conversions
Apr 19, 2025
-
Life Cycle Of A Plant Bean
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 45 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.