5 2 As A Mixed Number
Kalali
Apr 13, 2025 · 5 min read
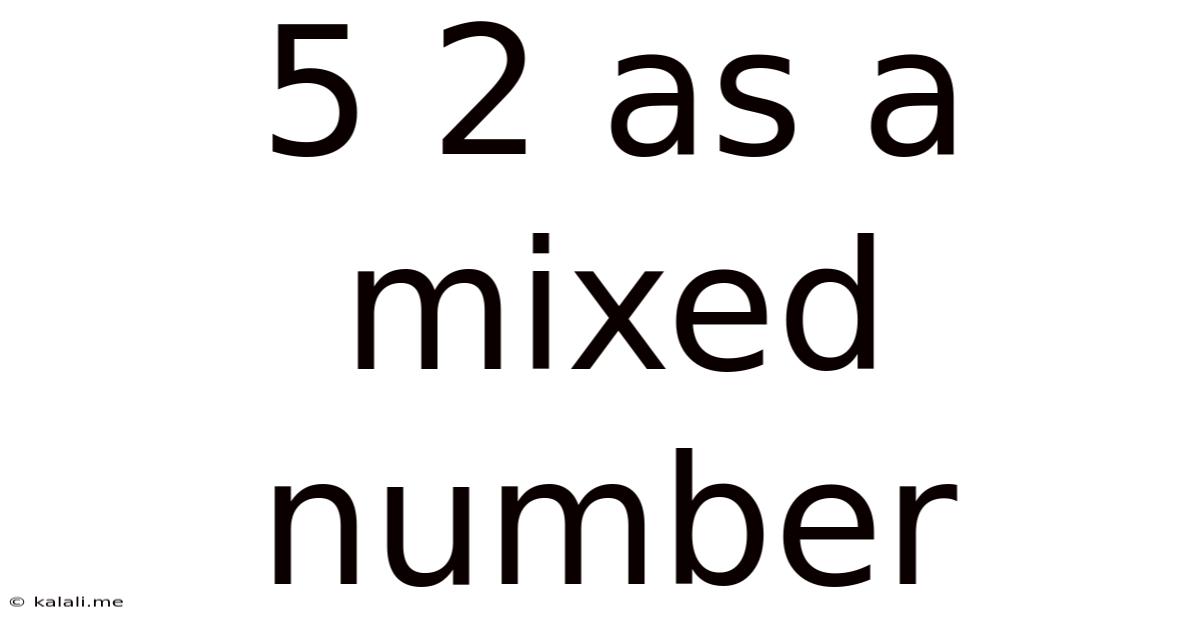
Table of Contents
Understanding 5/2 as a Mixed Number: A Comprehensive Guide
The fraction 5/2, often encountered in mathematics, represents five parts out of two equal parts. This form, known as an improper fraction, where the numerator (5) is larger than the denominator (2), isn't always the most convenient format for calculations or understanding. Converting it to a mixed number provides a clearer representation, making it easier to visualize and work with. This article will thoroughly explain the process of converting 5/2 into a mixed number, explore its applications, and delve into related concepts to enhance your understanding of fractions.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator smaller than its denominator. For instance, 1 ¾, 2 ⅓, and 5 ⅛ are all examples of mixed numbers. They offer a more intuitive way to represent quantities larger than one whole unit. Understanding mixed numbers is crucial in various fields, from cooking (measuring ingredients) to construction (measuring materials) and even advanced mathematical concepts.
Converting 5/2 to a Mixed Number: Step-by-Step Guide
The conversion of 5/2 to a mixed number involves two simple steps:
-
Division: Divide the numerator (5) by the denominator (2). 5 ÷ 2 = 2 with a remainder of 1.
-
Constructing the Mixed Number: The quotient (2) becomes the whole number part of the mixed number. The remainder (1) becomes the numerator of the proper fraction, and the denominator remains the same (2).
Therefore, 5/2 as a mixed number is 2 ½.
Visual Representation of 5/2
Imagine you have five halves of a pizza. You can easily combine two halves to form one whole pizza. This leaves you with one remaining half. This visual representation perfectly aligns with the mixed number 2 ½. This concrete example helps solidify the abstract concept of fraction conversion.
Why Use Mixed Numbers?
While improper fractions are perfectly valid mathematical representations, mixed numbers offer several advantages:
-
Intuitive Understanding: Mixed numbers are easier to grasp intuitively. It's simpler to understand "2 ½ pizzas" than "5/2 pizzas."
-
Real-World Applications: Many real-world measurements and quantities are expressed using mixed numbers. For example, measuring the length of a board as 3 ¼ feet is more practical than expressing it as 13/4 feet.
-
Simplified Calculations: In some calculations, using mixed numbers can simplify the process, especially when dealing with addition and subtraction of fractions with different denominators.
-
Improved Communication: Using mixed numbers enhances clarity and communication, particularly when explaining mathematical concepts to others.
Further Exploration of Fractions and Mixed Numbers
Beyond the basic conversion, let's explore related concepts that build a more comprehensive understanding of fractions and mixed numbers:
Equivalent Fractions
Equivalent fractions represent the same value even though they look different. For instance, ½ is equivalent to 2/4, 3/6, 4/8, and so on. Understanding equivalent fractions is vital when adding and subtracting fractions with different denominators. To find equivalent fractions, you simply multiply or divide both the numerator and denominator by the same non-zero number.
Simplifying Fractions
Simplifying, or reducing, a fraction means expressing it in its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example, 6/8 can be simplified to ¾ by dividing both the numerator and denominator by 2 (their GCD). Simplifying fractions makes them easier to work with and understand.
Adding and Subtracting Mixed Numbers
Adding and subtracting mixed numbers requires a slightly different approach than adding and subtracting proper fractions. One common method involves converting the mixed numbers into improper fractions, performing the addition or subtraction, and then converting the result back into a mixed number. Alternatively, you can add or subtract the whole number parts separately and then work with the fractional parts, potentially needing to borrow or carry over fractions depending on the values.
Example: Adding Mixed Numbers
Let's add 2 ½ and 1 ¾:
-
Convert to Improper Fractions: 2 ½ = 5/2 and 1 ¾ = 7/4
-
Find a Common Denominator: The least common multiple of 2 and 4 is 4. Convert 5/2 to an equivalent fraction with a denominator of 4: 10/4.
-
Add the Improper Fractions: 10/4 + 7/4 = 17/4
-
Convert back to a Mixed Number: 17 ÷ 4 = 4 with a remainder of 1. Therefore, the result is 4 ¼.
Example: Subtracting Mixed Numbers
Let's subtract 1 ¾ from 2 ½:
-
Convert to Improper Fractions: 2 ½ = 5/2 and 1 ¾ = 7/4
-
Find a Common Denominator: Again, the least common multiple of 2 and 4 is 4. Convert 5/2 to 10/4.
-
Subtract the Improper Fractions: 10/4 - 7/4 = 3/4
This result is already a proper fraction, so no further conversion is needed.
Multiplying and Dividing Mixed Numbers
Multiplying and dividing mixed numbers often involves a similar process to adding and subtracting. It’s generally easier to convert mixed numbers into improper fractions before performing the multiplication or division. Afterward, you can convert the result back into a mixed number if needed.
Real-World Applications of 5/2 and Mixed Numbers
The fraction 5/2, or its equivalent mixed number 2 ½, appears in various real-world scenarios:
-
Cooking: A recipe might call for 2 ½ cups of flour.
-
Construction: Measuring lumber or other materials frequently involves mixed numbers.
-
Finance: Calculating interest or portions of payments often utilizes fractions and mixed numbers.
-
Data Analysis: Representing proportions or averages might involve mixed numbers.
-
Sports: Statistics, such as batting averages, are often represented using decimals, which can be easily converted from fractions and mixed numbers.
Conclusion:
Understanding the conversion of improper fractions like 5/2 to mixed numbers (2 ½) is essential for practical applications and further mathematical studies. This guide has provided a step-by-step explanation, visual representations, and explored related concepts, building a solid foundation for working with fractions and mixed numbers. Mastering these concepts significantly improves your mathematical skills and problem-solving abilities across various domains. Remember to practice regularly to solidify your understanding and apply these concepts effectively in diverse situations. The ability to seamlessly convert between improper fractions and mixed numbers demonstrates a fundamental grasp of fractional arithmetic, a skill that will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
What Is 1 6 In Fraction Form
Apr 14, 2025
-
What Is 7 Oz In Cups
Apr 14, 2025
-
What Is 30 Degrees C In Fahrenheit
Apr 14, 2025
-
Cuanto Es 58 Fahrenheit En Centigrados
Apr 14, 2025
-
2 5 Cm Is How Many Mm
Apr 14, 2025
Related Post
Thank you for visiting our website which covers about 5 2 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.