5 Is What Percent Of 8
Kalali
Mar 10, 2025 · 4 min read
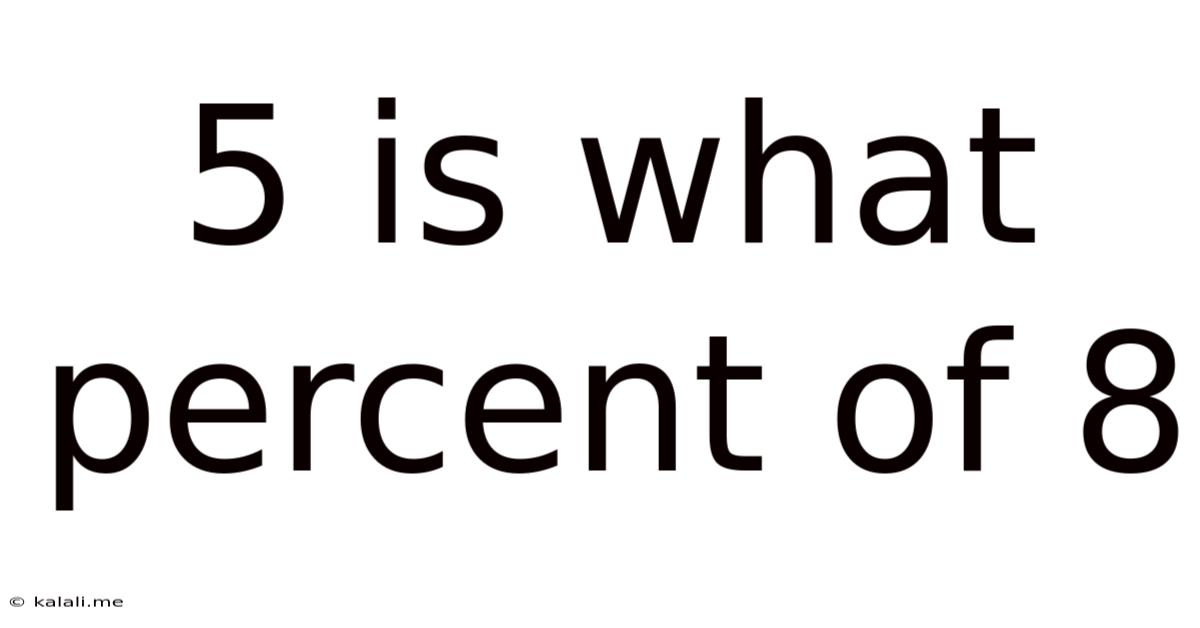
Table of Contents
5 is What Percent of 8? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide will delve into the question, "5 is what percent of 8?", providing not only the solution but also a detailed explanation of the underlying principles and various methods for solving percentage problems. We'll explore different approaches, including using proportions, the percentage formula, and even a visual representation to solidify your understanding. By the end of this article, you'll be equipped to confidently tackle any percentage calculation.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For instance, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Percentages are used to represent proportions or ratios, making it easier to compare different quantities.
Method 1: Using Proportions to Solve "5 is What Percent of 8?"
Proportions offer a clear and intuitive way to solve percentage problems. A proportion is an equation that states that two ratios are equal. In this case, we can set up a proportion to represent the relationship between 5 (the part) and 8 (the whole):
Part / Whole = Percentage / 100
Substituting the known values, we get:
5 / 8 = x / 100
Here, 'x' represents the unknown percentage we're trying to find. To solve for 'x', we can cross-multiply:
5 * 100 = 8 * x
500 = 8x
Now, divide both sides by 8:
x = 500 / 8
x = 62.5
Therefore, 5 is 62.5% of 8.
Method 2: Using the Percentage Formula
The percentage formula provides another straightforward approach:
Percentage = (Part / Whole) * 100
Again, substituting our values:
Percentage = (5 / 8) * 100
Percentage = 0.625 * 100
Percentage = 62.5%
This confirms our previous result. This formula is extremely versatile and can be used to solve a wide range of percentage problems.
Method 3: Visual Representation – Understanding the Concept
While the mathematical methods are precise, visualizing the problem can enhance understanding. Imagine a bar representing the whole (8). We want to find what percentage of this bar is represented by 5.
[Imagine a bar graph here, divided into 8 equal parts. 5 parts should be shaded.]
By dividing the bar into 8 equal parts, each part represents 1/8 of the whole. Since 5 parts are shaded, we can calculate the percentage as:
(5 parts / 8 total parts) * 100% = 62.5%
This visual representation reinforces the concept that a percentage represents a fraction of a whole.
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in many real-world scenarios. Here are a few examples:
- Discounts: If a store offers a 20% discount on an item originally priced at $80, the discount amount is (20/100) * $80 = $16. The final price would be $80 - $16 = $64.
- Taxes: Calculating sales tax involves finding a percentage of the total price. If the sales tax is 6% and the item costs $50, the tax amount is (6/100) * $50 = $3. The total cost would be $50 + $3 = $53.
- Grades and Scores: In education, percentages are frequently used to express scores and grades. A student scoring 80 out of 100 on a test has achieved an 80% score.
- Financial Analysis: Percentages play a vital role in financial statements, analyzing profit margins, growth rates, and investment returns. Understanding percentage changes allows for meaningful comparisons over time.
- Data Analysis: In statistical analysis, percentages help to present data clearly and concisely. For instance, expressing the percentage of respondents who favor a particular product simplifies the interpretation of survey results.
Advanced Percentage Problems: Building Upon the Fundamentals
Once you've mastered the basics, you can tackle more complex percentage problems. These often involve multiple steps and may require rearranging the percentage formula to solve for an unknown variable (part, whole, or percentage).
Example 1: Finding the Whole
-
Problem: 15% of a number is 3. What is the number?
-
Solution: We can adapt the percentage formula: Whole = (Part / Percentage) * 100. Substituting the values, we get: Whole = (3 / 15) * 100 = 20.
Example 2: Finding the Part
-
Problem: What is 35% of 60?
-
Solution: Part = (Percentage / 100) * Whole. Substituting the values, we get: Part = (35/100) * 60 = 21.
Example 3: Percentage Increase or Decrease
-
Problem: A price increased from $50 to $60. What is the percentage increase?
-
Solution: First, find the difference: $60 - $50 = $10. Then, calculate the percentage increase: (Increase / Original Value) * 100 = ($10 / $50) * 100 = 20%.
Mastering Percentages: Practice and Resources
The key to mastering percentage calculations is consistent practice. Work through various problems, starting with simple examples and gradually increasing the complexity. There are numerous online resources, including interactive exercises and quizzes, that can help you reinforce your understanding.
Conclusion: Beyond the Numbers
This comprehensive guide has explored the question, "5 is what percent of 8?", demonstrating multiple methods to arrive at the solution (62.5%). Beyond the specific answer, the goal is to equip you with a strong understanding of percentage calculations and their wide-ranging applications. By mastering these skills, you’ll enhance your problem-solving abilities and gain valuable insights in various fields. Remember that practice is key, and with consistent effort, you can confidently navigate the world of percentages.
Latest Posts
Latest Posts
-
How Many Liters Is In A Water Bottle
Jun 30, 2025
-
How Many Cups Of Milk Are In A Half Gallon
Jun 30, 2025
-
How Many Ritz Crackers In A Cup
Jun 30, 2025
-
How Many 16 9 Oz Bottles Make A Half Gallon
Jun 30, 2025
-
How Many Times Does 3 Go Into 24
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about 5 Is What Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.