5 Of 30 Is What Percent
Kalali
Apr 16, 2025 · 5 min read
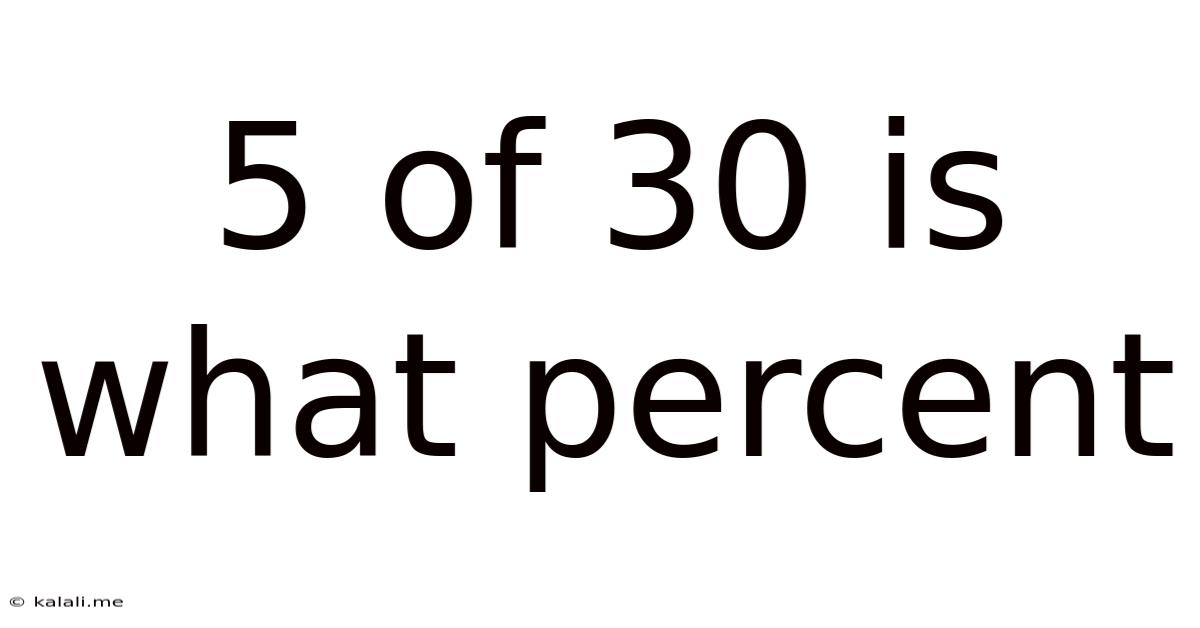
Table of Contents
5 out of 30 is What Percent? A Comprehensive Guide to Percentage Calculations
Meta Description: Learn how to calculate percentages with ease! This comprehensive guide explains how to find what percentage 5 out of 30 represents, covering various methods and providing practical examples for everyday use. Master percentage calculations and improve your math skills.
Finding the percentage that 5 represents out of 30 is a fundamental skill in mathematics with widespread applications in various fields, from calculating discounts and tax rates to understanding statistics and analyzing data. This guide will not only show you how to solve this specific problem (5 out of 30 is what percent?) but also equip you with the knowledge and techniques to tackle similar percentage calculations with confidence.
We'll explore multiple methods, breaking down the process step-by-step, ensuring clarity and understanding even for those who haven't worked with percentages extensively. Whether you're a student, a professional, or simply curious about percentages, this article will serve as a valuable resource.
Understanding Percentages
Before diving into the calculation, let's establish a solid foundation. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Understanding the basic relationship between fractions, decimals, and percentages is crucial. They are all different ways of expressing the same proportion. For instance:
- Fraction: 5/30
- Decimal: 0.1667 (approximately)
- Percentage: 16.67% (approximately)
Method 1: Using the Formula
The most straightforward method involves using a simple formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 5
- Whole: 30
Substituting these values into the formula:
(5 / 30) * 100 = 16.67% (approximately)
Therefore, 5 out of 30 is approximately 16.67%. The slight rounding is due to the repeating decimal in the fraction.
Method 2: Simplifying the Fraction
This method involves simplifying the fraction before converting it to a percentage. Simplifying makes the calculation easier and less prone to errors.
-
Simplify the Fraction: The fraction 5/30 can be simplified by dividing both the numerator (5) and the denominator (30) by their greatest common divisor, which is 5. This simplifies the fraction to 1/6.
-
Convert to Decimal: To convert the fraction 1/6 to a decimal, divide the numerator (1) by the denominator (6): 1 ÷ 6 ≈ 0.1667
-
Convert to Percentage: Multiply the decimal by 100: 0.1667 * 100 ≈ 16.67%
Again, we arrive at the same answer: approximately 16.67%.
Method 3: Using a Calculator
Modern calculators are designed to handle percentage calculations effortlessly. Most calculators have a percentage button (% key). The exact steps may vary depending on the calculator model, but the general process is as follows:
- Enter the fraction: Enter 5 ÷ 30.
- Press the percentage button: Press the % key.
- Read the result: The calculator will display the result as 16.66666...%, which rounds to approximately 16.67%.
This method provides a quick and efficient way to calculate percentages, especially for more complex calculations.
Understanding the Significance of Rounding
Notice that in all our calculations, we rounded the percentage to 16.67%. This is because the exact decimal representation of 5/30 is a repeating decimal (0.16666...). Rounding allows for a more manageable and practical representation of the percentage. The level of rounding depends on the context; sometimes, a higher degree of precision is required. For most everyday purposes, rounding to two decimal places is sufficient.
Real-World Applications of Percentage Calculations
Percentage calculations are indispensable in numerous real-world scenarios. Here are a few examples:
-
Sales and Discounts: Calculating discounts on products, understanding sale prices, and determining the final price after discounts. For instance, a 20% discount on a $100 item means a $20 reduction, resulting in a final price of $80.
-
Taxes and Interest: Calculating sales tax, income tax, interest on loans, and interest earned on savings accounts. These calculations involve applying a percentage to the base amount.
-
Statistics and Data Analysis: Percentages are used extensively in statistics to represent proportions, analyze data sets, and interpret results. For example, calculating the percentage of students who passed an exam, or the percentage change in a company's stock price.
-
Financial Planning: Percentages are vital in financial planning for budgeting, calculating investment returns, analyzing financial statements, and tracking progress towards financial goals.
-
Scientific Calculations: Percentages are used to express concentrations, error margins, and changes in various scientific experiments and analyses.
Advanced Percentage Calculations: Finding the Whole or the Part
While this article focuses on finding the percentage, understanding how to find the whole or the part when the percentage is known is equally important.
-
Finding the Whole: If you know the percentage and the part, you can find the whole by using the formula: Whole = (Part / Percentage) * 100
-
Finding the Part: If you know the percentage and the whole, you can find the part by using the formula: Part = (Percentage / 100) * Whole
Practice Problems
To solidify your understanding, try solving these practice problems:
- What percentage is 12 out of 60?
- What percentage is 7 out of 28?
- If 15% of a number is 30, what is the number?
- A shirt costs $50. If there is a 30% discount, what is the final price?
- A student scored 80 out of 100 on a test. What is their percentage score?
By practicing these problems, you will reinforce your understanding of percentage calculations and build your confidence in tackling various percentage-related problems.
Conclusion: Mastering Percentage Calculations
Understanding and applying percentage calculations is a valuable skill applicable across various domains. This guide has provided a comprehensive approach to solving problems involving percentages, encompassing different methods and highlighting the importance of understanding the underlying concepts. Remember that consistent practice is key to mastering any mathematical skill, and by applying the methods described in this article, you'll be well-equipped to handle percentage calculations confidently and accurately. So, the next time you encounter a question like "5 out of 30 is what percent?", you'll be able to solve it with ease and precision.
Latest Posts
Latest Posts
-
Is Ice Melts A Physical Or Chemical Change
Apr 18, 2025
-
How To Solve For Vertical Angles
Apr 18, 2025
-
Cuanto Son 3 Metros En Pies
Apr 18, 2025
-
What Is 20 Off Of 80
Apr 18, 2025
-
How Many Ounces Is 1 2 A Pound
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 5 Of 30 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.