5 Out Of 12 As A Percentage
Kalali
Apr 09, 2025 · 5 min read
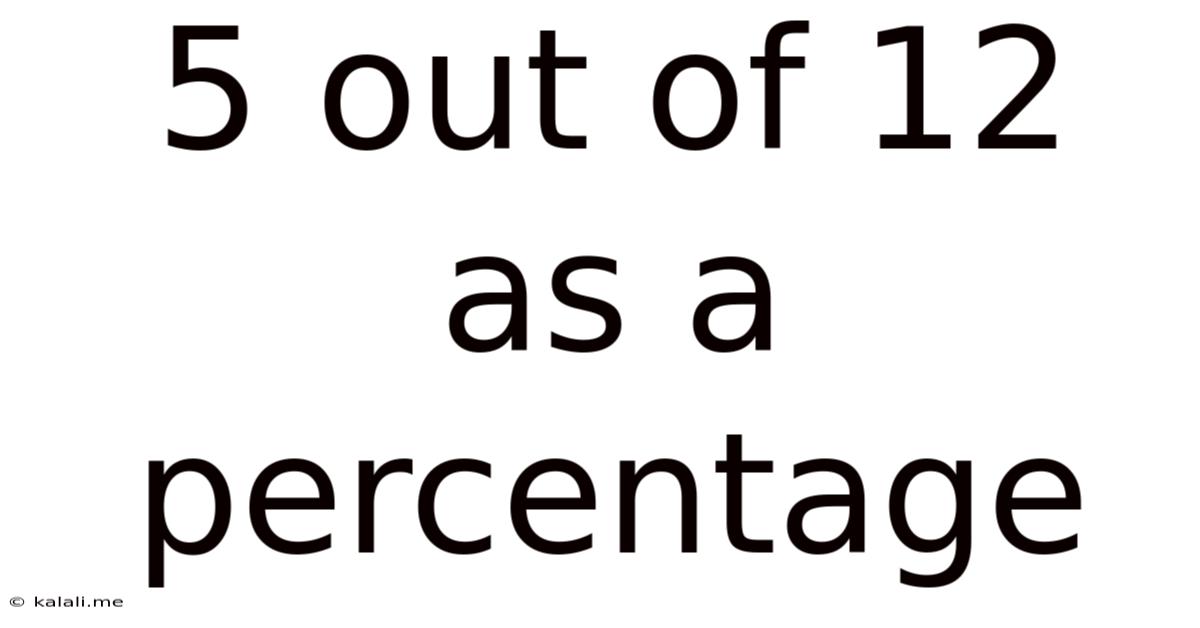
Table of Contents
5 Out of 12 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts in a shop to analyzing financial reports. This article provides a thorough explanation of how to calculate 5 out of 12 as a percentage, along with various methods and practical applications. We'll also delve into the broader context of percentage calculations and explore how to tackle similar problems effectively. Understanding this seemingly simple calculation can unlock a deeper understanding of proportions and ratios, crucial skills for both everyday life and professional settings.
What is a Percentage?
Before diving into the calculation, let's clarify what a percentage actually represents. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per hundred," indicating the proportion of a whole. For instance, 50% means 50 out of 100, or half. Understanding this foundational concept is essential for grasping percentage calculations.
Calculating 5 Out of 12 as a Percentage: Three Different Approaches
There are several ways to determine what percentage 5 out of 12 represents. We will explore three common methods:
Method 1: Using the Fraction Method
This is perhaps the most straightforward approach. We begin by expressing "5 out of 12" as a fraction: 5/12. To convert this fraction to a percentage, we need to transform the denominator (the bottom number) into 100. We do this by multiplying both the numerator (the top number) and the denominator by the same number that will result in a denominator of 100. However, since 12 doesn't divide evenly into 100, we'll use a slightly different approach.
First, we divide the numerator by the denominator: 5 ÷ 12 = 0.416666...
This decimal represents the proportion of 5 out of 12. To convert this decimal to a percentage, we simply multiply by 100: 0.416666... × 100 = 41.6666...%
Rounding to two decimal places, we get 41.67%.
Method 2: Using Proportions
The proportion method offers another route to the solution. We can set up a proportion to solve for the unknown percentage (x):
5/12 = x/100
To solve for x, we cross-multiply:
12x = 500
Then, divide both sides by 12:
x = 500/12 = 41.6666...
Again, multiplying by 100 gives us the percentage: 41.67% (rounded to two decimal places). This method highlights the relationship between fractions and percentages, emphasizing their interchangeable nature in representing proportions.
Method 3: Using a Calculator
Modern calculators simplify percentage calculations significantly. Most calculators have a percentage function. Simply enter 5 ÷ 12 and then multiply the result by 100. The calculator will directly display the percentage, saving you the manual steps. This method is efficient for quick calculations, but understanding the underlying principles remains crucial for problem-solving in more complex scenarios.
Practical Applications of Percentage Calculations: Real-world Examples
Understanding how to calculate percentages extends far beyond simple arithmetic exercises. It's a fundamental skill with applications in numerous fields:
-
Finance: Calculating interest rates, loan repayments, investment returns, and tax rates all rely heavily on percentage calculations. Understanding how percentage changes impact your finances is crucial for informed financial decision-making. For example, calculating the percentage increase or decrease in your investment portfolio over a specific period.
-
Retail and Sales: Discounts, markups, and sales tax are all expressed as percentages. Calculating the final price of an item after a discount or adding sales tax requires understanding percentage calculations. Determining the percentage profit margin on a product is also a key aspect of retail business analysis.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. Representing survey results, analyzing demographic trends, and understanding probability all involve percentage calculations. For example, determining the percentage of respondents who favor a particular product in a market research survey.
-
Science and Engineering: Percentages are used extensively in scientific measurements and calculations, such as calculating error margins in experiments or expressing the concentration of a solution.
-
Education: Calculating grades, assessing test performance, and understanding progress are all based on percentages. Converting raw scores to percentages for standardized tests requires accurate percentage calculations.
Beyond 5 Out of 12: Mastering Percentage Calculations
The methods described above can be applied to any fraction to calculate its percentage equivalent. For example, if you need to calculate 7 out of 15 as a percentage, you would follow the same steps:
- Fraction: 7/15
- Division: 7 ÷ 15 ≈ 0.4667
- Percentage: 0.4667 × 100 ≈ 46.67%
This versatile approach allows you to tackle a wide range of percentage problems, from simple calculations to more complex scenarios.
Understanding Percentage Change: A Crucial Extension
Beyond calculating the percentage representation of a fraction, understanding percentage change is vital. Percentage change measures the relative difference between two values. It's calculated using the formula:
[(New Value - Old Value) / Old Value] × 100
For example, if a product's price increased from $100 to $120, the percentage increase is:
[(120 - 100) / 100] × 100 = 20%
Similarly, you can calculate percentage decreases. Understanding percentage change allows you to analyze trends, growth rates, and other dynamic data effectively.
Common Mistakes to Avoid in Percentage Calculations
While percentage calculations are straightforward, certain common errors can lead to inaccurate results:
-
Incorrect Order of Operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Rounding Errors: Rounding off numbers too early in the calculation process can accumulate errors, leading to inaccuracies in the final result. It's generally recommended to round off only at the final step.
-
Confusing Percentage Increase and Decrease: Clearly distinguish between calculating a percentage increase and a percentage decrease. The formulas and interpretations differ.
-
Not Considering the Base: Always remember that the percentage is calculated relative to a base value. Misinterpreting the base value can lead to incorrect calculations.
Conclusion: The Importance of Mastering Percentages
Mastering percentage calculations is not just about solving mathematical problems; it's about developing a deeper understanding of proportions, ratios, and relative changes. This skill is invaluable across various disciplines and everyday situations. By understanding the different methods of calculation, their applications, and common pitfalls, you can confidently tackle percentage problems and utilize this essential skill to your advantage in both personal and professional settings. Remember, practice is key to mastering this fundamental skill and building a solid foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How To Solve A Log Without A Calculator
Apr 18, 2025
-
What Is 10 Degrees Celsius On The Fahrenheit Scale
Apr 18, 2025
-
How Much Is 187 Ml In Ounces
Apr 18, 2025
-
Cuanto Es 5 6 Pies En Metros
Apr 18, 2025
-
How Many Inches Are In 180 Cm
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 12 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.