5 X 5 X 5 X 5
Kalali
Jul 01, 2025 · 6 min read
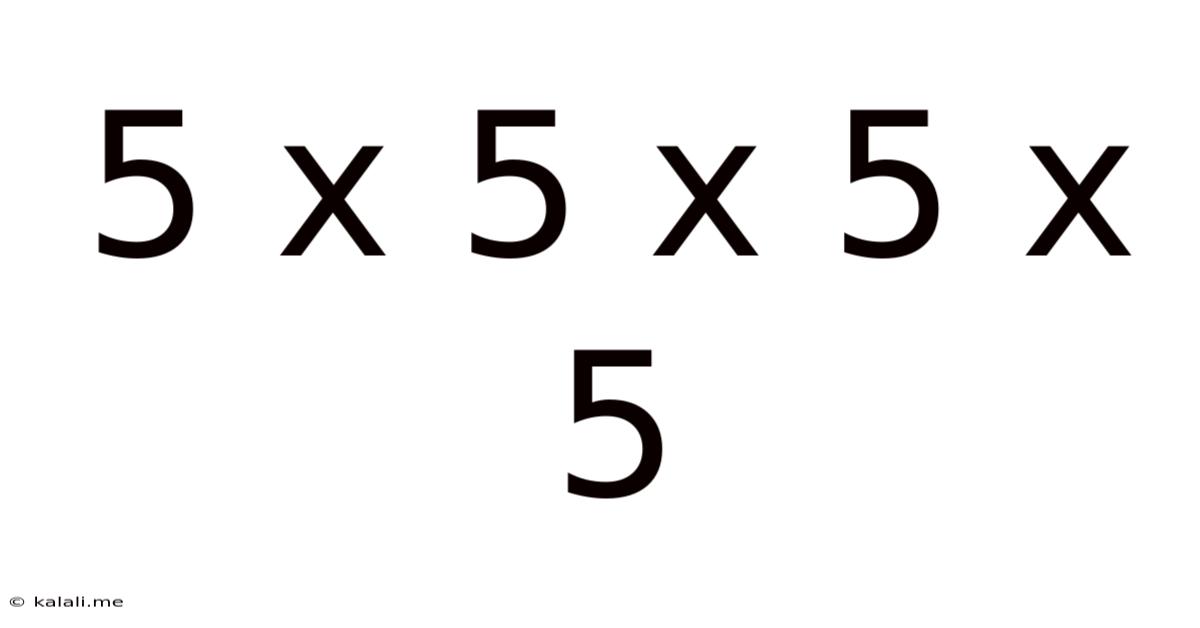
Table of Contents
Decoding 5 x 5 x 5 x 5: Exploring the Mathematical, Philosophical, and Practical Implications of a Simple Equation
This seemingly simple equation, 5 x 5 x 5 x 5, holds more depth than meets the eye. At its core, it's a basic multiplication problem, easily solved with a calculator. But beyond the immediate answer of 625, lies a wealth of opportunities to explore mathematical concepts, philosophical implications, and practical applications across various fields. This article delves into these aspects, unraveling the multifaceted nature of this seemingly straightforward calculation.
Meta Description: Uncover the hidden depths of 5 x 5 x 5 x 5! This article explores the mathematical foundations, philosophical implications, and practical applications of this simple equation, revealing its surprising complexity and relevance across diverse fields.
I. The Mathematical Foundation: Beyond Simple Multiplication
At its most basic level, 5 x 5 x 5 x 5 represents repeated multiplication. It's equivalent to 5⁴ (5 raised to the power of 4), which is a fundamental concept in algebra and exponentiation. This equation demonstrates the rapid growth achievable through exponential functions, a concept crucial in understanding various phenomena, from compound interest to population growth.
1.1 Exponentiation and its Significance: The use of exponents significantly simplifies the expression of repeated multiplication. Instead of writing out five 5s multiplied together, we concisely represent it as 5⁴. This notation is essential for advanced mathematical concepts like logarithms, calculus, and complex number theory. Understanding exponentiation allows us to grasp the rapid growth inherent in exponential functions, a key element in modeling real-world phenomena.
1.2 Prime Factorization and Number Theory: The number 625, the result of 5 x 5 x 5 x 5, has a unique prime factorization. It's simply 5⁴, meaning its only prime factor is 5. This simplicity highlights its significance in number theory. Analyzing prime factorizations helps us understand the fundamental building blocks of numbers and their relationships. The concept of prime factorization has far-reaching implications in cryptography and other areas of computer science.
1.3 Modular Arithmetic and its Applications: Modular arithmetic involves performing arithmetic operations within a specific range (modulo). For example, calculating 625 modulo 10 gives us 5 (the remainder when 625 is divided by 10). This seemingly simple operation has crucial applications in cryptography, particularly in generating and verifying digital signatures and ensuring data security.
1.4 Relationships to other Mathematical Concepts: The number 625 is also connected to other mathematical concepts. For instance, it's a perfect square (25²), a perfect fifth power (5⁵), and a member of various number sequences. Exploring these connections deepens our understanding of number patterns and relationships.
II. Philosophical Implications: Exploring the Nature of Growth and Repetition
The equation 5 x 5 x 5 x 5, beyond its numerical value, offers a platform for philosophical contemplation. The repeated multiplication of 5 can be interpreted as a metaphor for various phenomena:
2.1 The Power of Exponential Growth: The rapid increase from 5 to 625 illustrates the potential for exponential growth. This principle has profound implications across diverse areas, from the growth of populations and economies to the spread of information and ideas. It also highlights the importance of understanding and managing exponential growth to avoid unintended consequences.
2.2 Repetition and its Significance: The repeated multiplication of the same number (5) emphasizes the significance of repetition in achieving significant outcomes. This concept finds resonance in various aspects of life, from the importance of consistent effort in achieving goals to the power of repeated practice in mastering a skill. The cumulative effect of repeated actions is a fundamental concept in many fields.
2.3 The Concept of Scale: The jump from 5 to 625 illustrates the concept of scale. A seemingly small initial value can, through repeated multiplication, lead to a remarkably large outcome. This concept is relevant across fields, from physics (understanding the scale of the universe) to economics (analyzing market growth).
2.4 Simplicity and Complexity: The equation itself is strikingly simple, yet its implications are far-reaching and complex. This duality highlights the often-hidden complexities that lie beneath the surface of simple ideas and expressions.
III. Practical Applications Across Diverse Fields
The mathematical principles illustrated by 5 x 5 x 5 x 5 have practical applications across various fields:
3.1 Finance and Investment: Compound interest calculations heavily rely on exponential growth, similar to the principle of 5 x 5 x 5 x 5. Understanding this concept is crucial for making informed financial decisions, particularly in long-term investment strategies. The exponential nature of compound interest can lead to significant growth over time.
3.2 Computer Science and Programming: Exponential growth and algorithms are central to computer science. Many algorithms have exponential time complexity, meaning their processing time increases exponentially with input size. Understanding exponential growth is crucial for designing efficient algorithms and optimizing computer programs. Furthermore, binary systems, fundamental to computing, utilize powers of 2, which share a conceptual link with exponential growth.
3.3 Physics and Engineering: Exponential functions are used to model various physical phenomena, including radioactive decay, population dynamics, and the spread of epidemics. Understanding these models is crucial for making accurate predictions and developing effective strategies. Exponential decay, for instance, is essential in understanding the lifespan of radioactive materials.
3.4 Biology and Ecology: Population growth often follows exponential patterns, particularly when resources are abundant. Understanding exponential growth is crucial for managing populations, predicting ecological changes, and developing conservation strategies. The rapid growth of bacterial colonies, for example, demonstrates exponential growth in action.
3.5 Data Analysis and Statistics: Exponential distributions are commonly used to model data in various fields. Understanding these distributions is essential for analyzing data, making accurate inferences, and drawing meaningful conclusions. The concept of exponential decay is crucial in the study of survival analysis, where it is used to model the lifespan of individuals or components.
IV. Exploring Variations and Extensions
The simplicity of 5 x 5 x 5 x 5 allows for exploration of variations and extensions:
4.1 Changing the Base: Instead of 5, we can explore different base numbers (e.g., 2 x 2 x 2 x 2 = 16, 10 x 10 x 10 x 10 = 10000). This allows for a comparative analysis of exponential growth with different base numbers.
4.2 Changing the Exponent: Instead of 4, we can use different exponents (e.g., 5¹ = 5, 5² = 25, 5³ = 125, 5⁵ = 3125). This explores the relationship between the exponent and the resulting value, highlighting the rapid growth of exponential functions.
4.3 Exploring other mathematical operations: We can extend the concept beyond multiplication and explore other mathematical operations, such as addition, subtraction, division, or even more complex operations like integration and differentiation, applied to functions involving powers of 5.
4.4 Connecting to Geometry: The number 625 can be connected to geometric concepts. For instance, it could represent the area of a square with sides of 25 units or the volume of a cube with sides of 5 units. This connection highlights the interplay between algebra and geometry.
V. Conclusion: The Enduring Relevance of a Simple Equation
The equation 5 x 5 x 5 x 5, while seemingly simple, offers a gateway to exploring fundamental mathematical concepts, philosophical implications, and practical applications across diverse fields. From understanding exponential growth and its impact on finance, computer science, and biology to appreciating the power of repetition and the interplay between simplicity and complexity, this seemingly straightforward calculation holds a wealth of knowledge and insight. Its enduring relevance underscores the importance of exploring even the most basic mathematical expressions to unlock deeper understanding and appreciation for the intricate world around us. Further exploration of these concepts can lead to a richer understanding of mathematics and its pervasive influence on our world.
Latest Posts
Latest Posts
-
Are Sour Cream And Onion Lays Gluten Free
Jul 31, 2025
-
Why Couldnt The Chicken Find Her Egg
Jul 31, 2025
-
Pale Yellow Or Buff Colored Cloth Originally From China
Jul 31, 2025
-
How Many Tablespoons In A Ranch Seasoning Packet
Jul 31, 2025
-
How Many Cubic In In A Gallon
Jul 31, 2025
Related Post
Thank you for visiting our website which covers about 5 X 5 X 5 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.