5 X 5 X 5 X 5 X 5
Kalali
Jul 03, 2025 · 5 min read
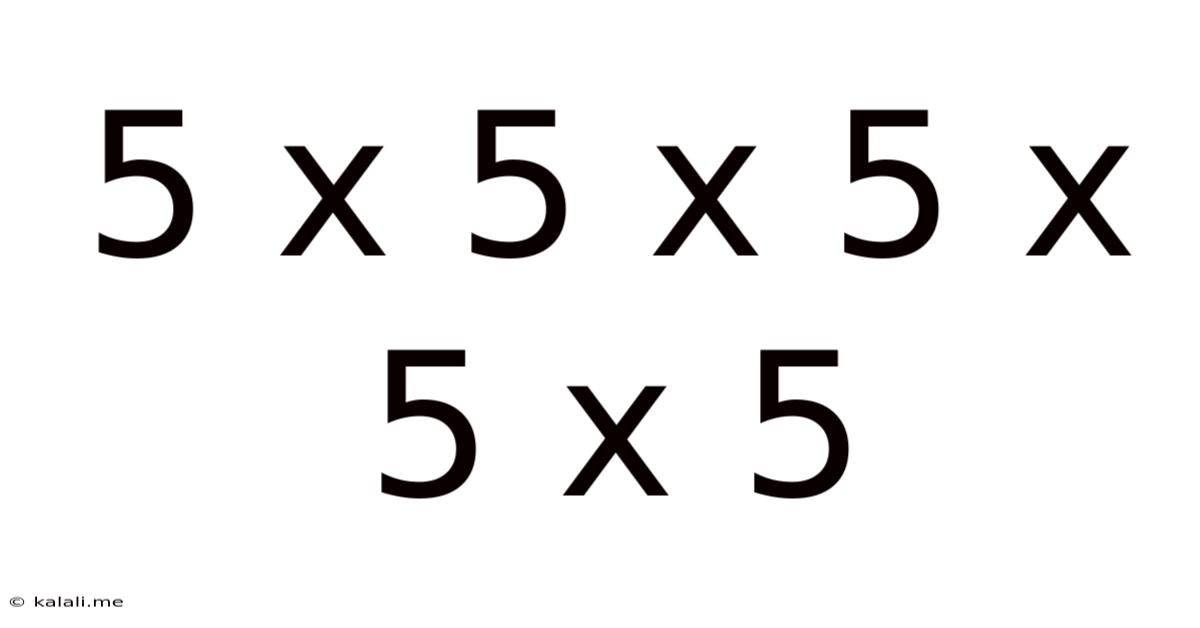
Table of Contents
Decoding 5 x 5 x 5 x 5 x 5: Exploring the Mathematical and Conceptual Dimensions of Repeated Multiplication
This seemingly simple mathematical expression, 5 x 5 x 5 x 5 x 5, opens a door to a fascinating exploration of exponential growth, computational methods, and even philosophical interpretations of repeated processes. At its core, it represents the repeated multiplication of the number 5, five times. This article will delve into the various aspects of this expression, examining its calculation, applications, and the broader mathematical concepts it embodies. Understanding this seemingly simple calculation can unlock a deeper appreciation for the power and elegance of mathematics.
1. The Straightforward Calculation: Exponents and Their Power
The most direct approach to solving 5 x 5 x 5 x 5 x 5 is through repeated multiplication. We begin with 5 x 5 = 25. Then, we multiply this result by the next 5: 25 x 5 = 125. Continuing this process, we get 125 x 5 = 625, and finally 625 x 5 = 3125. Therefore, the answer to 5 x 5 x 5 x 5 x 5 is 3125.
However, this method becomes cumbersome with larger numbers or more repetitions. This is where the concept of exponents comes in handy. The expression 5 x 5 x 5 x 5 x 5 can be written more concisely as 5⁵, where the superscript 5 (exponent) indicates that 5 is multiplied by itself five times. This exponential notation is crucial in mathematics and computer science for representing repeated multiplication efficiently.
2. Exploring Exponential Growth: A Visual Representation
The repeated multiplication inherent in 5⁵ exemplifies exponential growth. This is a pattern where the quantity increases at an accelerating rate. Imagine a scenario where a bacteria population doubles every hour. This is analogous to repeated multiplication. The initial population grows exponentially, showcasing the rapid increase characteristic of exponential functions.
Visualizing exponential growth can help us grasp its magnitude. Consider plotting the results of repeated multiplications of 5:
- 5¹ = 5
- 5² = 25
- 5³ = 125
- 5⁴ = 625
- 5⁵ = 3125
If we were to graph these values, we'd observe a curve that steeply increases, illustrating the hallmark of exponential growth. This growth is significantly faster than linear growth, where the increase is constant.
3. Computational Approaches: Beyond Manual Calculation
While manual calculation works well for smaller exponents, larger exponents require more sophisticated methods. Calculators and computer programs readily handle these calculations. Programming languages like Python provide built-in functions to calculate exponents (e.g., 5**5 in Python returns 3125). These tools are invaluable for tackling complex mathematical problems involving exponentiation.
The efficiency of computational methods is particularly crucial in fields like cryptography, where large exponents are used in encryption algorithms. The speed and accuracy of these computations are critical for securing data transmission and storage.
4. Applications Across Diverse Fields: From Science to Finance
The concept of repeated multiplication, and therefore the understanding of expressions like 5⁵, extends far beyond basic arithmetic. Its applications span various disciplines:
-
Compound Interest: In finance, compound interest calculations rely heavily on exponential growth. The principal amount grows exponentially over time due to repeated interest accrual. Understanding 5⁵ helps in grasping the power of compounding over multiple periods.
-
Scientific Modeling: Exponential functions are frequently used to model various phenomena in science, such as radioactive decay, population growth, and the spread of diseases. Solving equations involving exponents is essential for predicting future trends and understanding natural processes.
-
Computer Science: Exponents are fundamental in computer science, particularly in algorithms and data structures. Binary numbers, the foundation of digital computing, involve repeated multiplication by 2 (e.g., 2⁵ represents 32 in binary). Understanding exponents is crucial for optimizing algorithms and managing large datasets.
-
Game Theory and Probability: Probability calculations often involve repeated multiplication, particularly when dealing with independent events. For example, the probability of getting heads five times in a row when flipping a fair coin is (1/2)⁵, a direct application of exponential principles.
5. Beyond the Numbers: Philosophical and Conceptual Extensions
The repeated multiplication represented by 5⁵ offers avenues for broader conceptual exploration:
-
Iteration and Recursion: The process of repeatedly multiplying by 5 is an example of iteration – repeating a process multiple times. This concept is fundamental in computer programming (loops) and also relates to recursive functions, where a function calls itself within its definition. Understanding 5⁵ helps conceptualize these fundamental programming constructs.
-
The Power of Repetition: The expression highlights the immense power of repetition. Starting with a relatively small number (5), repeated multiplication leads to a substantially larger number (3125). This demonstrates how small, incremental changes, repeated consistently, can lead to significant results over time. This principle applies to various aspects of life, from personal growth to societal development.
-
Mathematical Elegance and Simplicity: The elegance of mathematical notation, as exemplified by the concise representation 5⁵, is noteworthy. A complex process is simplified to a neat, easily understandable form. This underscores the power and beauty inherent in mathematical structures and their ability to capture complex processes efficiently.
6. Further Exploration: Expanding the Concepts
The understanding of 5⁵ can be further expanded by exploring related mathematical concepts:
-
Logarithms: Logarithms are the inverse of exponents. If 5⁵ = 3125, then the logarithm base 5 of 3125 is 5 (log₅(3125) = 5). Understanding logarithms is essential for solving exponential equations and analyzing data with exponential trends.
-
Complex Numbers: Exponents can also be applied to complex numbers, extending their use beyond real numbers. This leads to fascinating applications in fields like electrical engineering and signal processing.
-
Higher-Dimensional Mathematics: The concept of exponentiation extends to higher-dimensional spaces and matrices, forming the basis for advanced mathematical concepts crucial in areas such as linear algebra and quantum mechanics.
Conclusion: The Unfolding Significance of a Simple Expression
The simple expression 5 x 5 x 5 x 5 x 5, or its concise equivalent 5⁵, serves as a gateway to a wealth of mathematical concepts and applications. From straightforward calculation to complex scientific modeling, this seemingly basic expression demonstrates the power of repeated multiplication and the profound implications of exponential growth. Its exploration reveals not only the mechanics of mathematics but also the elegance, efficiency, and far-reaching applications inherent in this fundamental mathematical concept. Understanding 5⁵ is not merely about obtaining the answer 3125; it's about appreciating the broader mathematical principles and their relevance across various fields of study and everyday life.
Latest Posts
Latest Posts
-
How Long Can You Use Mayonnaise After The Expiration Date
Jul 31, 2025
-
How Far Is Pigeon Forge Tennessee From Nashville
Jul 31, 2025
Related Post
Thank you for visiting our website which covers about 5 X 5 X 5 X 5 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.