6 5 As A Mixed Number
Kalali
Apr 05, 2025 · 6 min read
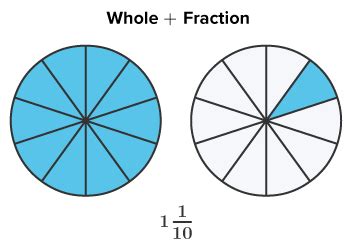
Table of Contents
6 5 as a Mixed Number: A Comprehensive Guide
Understanding mixed numbers is fundamental in mathematics, particularly in fractions and arithmetic operations. This article delves deep into the concept of representing improper fractions as mixed numbers, specifically focusing on the example of 6/5. We'll explore various methods to convert this improper fraction into a mixed number, providing detailed explanations and practical examples to solidify your understanding. We will also explore the practical applications of understanding mixed numbers and offer tips for mastering this essential mathematical concept.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For instance, 1/2, 3/4, and 2/5 are all proper fractions. In contrast, an improper fraction has a numerator that is greater than or equal to the denominator, such as 6/5, 7/3, or 10/10. Mixed numbers provide a more intuitive way to represent quantities greater than one but not a whole number.
Converting 6/5 to a Mixed Number: Step-by-Step Guide
The improper fraction 6/5 represents a quantity larger than one. To convert it into a mixed number, we need to determine how many whole numbers are contained within the fraction and the remaining fractional part. Here's a step-by-step process:
Method 1: Division
This is the most straightforward method. Divide the numerator (6) by the denominator (5):
-
Divide: 6 ÷ 5 = 1 with a remainder of 1.
-
Whole Number: The quotient (1) becomes the whole number part of the mixed number.
-
Fractional Part: The remainder (1) becomes the numerator of the fractional part, and the denominator remains the same (5).
-
Mixed Number: Therefore, 6/5 is equal to 1 1/5.
Method 2: Visual Representation
Imagine you have six slices of pizza, and each pizza is cut into five slices. You can assemble one whole pizza (5 slices) and have one slice left over. This visually represents the mixed number 1 1/5.
Method 3: Repeated Subtraction
Alternatively, repeatedly subtract the denominator from the numerator until you reach a number less than the denominator:
-
Subtract: 6 - 5 = 1
-
Whole Number: The number of times you subtracted the denominator (once) is the whole number (1).
-
Fractional Part: The remainder (1) becomes the numerator of the fraction, and the denominator remains (5).
-
Mixed Number: This again gives us the mixed number 1 1/5.
Understanding the Components of the Mixed Number 1 1/5
Let's break down the mixed number 1 1/5:
-
1: This represents one whole unit. Think of it as a complete pizza.
-
1/5: This represents one-fifth of a unit. Think of it as one slice from a pizza that was cut into five slices.
Therefore, 1 1/5 visually represents one whole pizza and one-fifth of another pizza.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in everyday situations and various fields:
-
Cooking: Recipes often call for mixed numbers of cups or teaspoons of ingredients (e.g., 2 1/2 cups of flour).
-
Measurement: Measuring length, weight, or volume often involves mixed numbers (e.g., 3 3/4 inches).
-
Construction: Blueprints and construction plans frequently use mixed numbers to specify dimensions.
-
Time: Representing time often uses mixed numbers, such as 1 hour and 15 minutes (1 1/4 hours).
-
Data Analysis: Mixed numbers can appear in datasets and statistical representations.
-
Geometry: Mixed numbers are frequently used to represent measurements of length, area, and volume in geometric problems.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to know how to convert a mixed number back into an improper fraction. Let's reverse the process with 1 1/5:
-
Multiply: Multiply the whole number (1) by the denominator (5): 1 * 5 = 5
-
Add: Add the result (5) to the numerator (1): 5 + 1 = 6
-
Improper Fraction: The sum (6) becomes the numerator, and the denominator remains the same (5). This gives us the improper fraction 6/5.
Working with Mixed Numbers: Addition and Subtraction
Adding and subtracting mixed numbers requires a clear understanding of their components. Let's explore this with an example:
Example: Add 2 1/2 and 1 1/4
-
Convert to Improper Fractions: Convert both mixed numbers into improper fractions:
- 2 1/2 = (2 * 2 + 1) / 2 = 5/2
- 1 1/4 = (1 * 4 + 1) / 4 = 5/4
-
Find a Common Denominator: Find the least common denominator (LCD) for the fractions: the LCD of 2 and 4 is 4.
-
Rewrite Fractions: Rewrite the fractions with the common denominator:
- 5/2 = 10/4
- 5/4 remains 5/4
-
Add: Add the fractions: 10/4 + 5/4 = 15/4
-
Convert Back to Mixed Number: Convert the improper fraction back to a mixed number: 15/4 = 3 3/4
Therefore, 2 1/2 + 1 1/4 = 3 3/4
Working with Mixed Numbers: Multiplication and Division
Multiplication and division of mixed numbers also involve similar steps, typically requiring conversion to improper fractions before performing the operations.
Example (Multiplication): Multiply 2 1/2 by 1 1/4
-
Convert to Improper Fractions: Convert both mixed numbers into improper fractions:
- 2 1/2 = 5/2
- 1 1/4 = 5/4
-
Multiply: Multiply the numerators and the denominators: (5/2) * (5/4) = 25/8
-
Convert Back to Mixed Number: Convert the improper fraction back to a mixed number: 25/8 = 3 1/8
Therefore, 2 1/2 * 1 1/4 = 3 1/8
Example (Division): Divide 2 1/2 by 1 1/4
-
Convert to Improper Fractions: Convert both mixed numbers into improper fractions:
- 2 1/2 = 5/2
- 1 1/4 = 5/4
-
Invert and Multiply: Invert the second fraction (divisor) and multiply: (5/2) * (4/5) = 20/10
-
Simplify: Simplify the resulting fraction: 20/10 = 2
Therefore, 2 1/2 ÷ 1 1/4 = 2
Mastering Mixed Numbers: Tips and Practice
Mastering mixed numbers takes practice. Here are some helpful tips:
-
Practice Regularly: The more you practice converting between improper fractions and mixed numbers, and performing arithmetic operations, the more comfortable you'll become.
-
Visual Aids: Use visual aids like diagrams or real-world objects to help understand the concept.
-
Step-by-Step Approach: Follow the steps carefully when converting and performing calculations.
-
Check Your Work: Always check your work to ensure accuracy.
-
Seek Help: Don't hesitate to ask for help if you're struggling.
-
Utilize Online Resources: Many online resources and educational websites offer interactive exercises and tutorials to practice working with fractions and mixed numbers.
By understanding the principles outlined above and dedicating time to practice, you can build a solid foundation in working with mixed numbers and apply this essential mathematical skill effectively in various real-world applications. Remember that consistent practice is key to mastering this crucial aspect of mathematics.
Latest Posts
Latest Posts
-
How To Confirm Unit Of Measure Xometools
Apr 06, 2025
-
65 6 As A Mixed Number
Apr 06, 2025
-
What Is 8 Pounds In Ounces
Apr 06, 2025
-
What Is A 22 Out Of 25
Apr 06, 2025
-
How Much Is 69 Inches In Feet
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about 6 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
