6 Divided By 9 As A Fraction
Kalali
Aug 25, 2025 · 5 min read
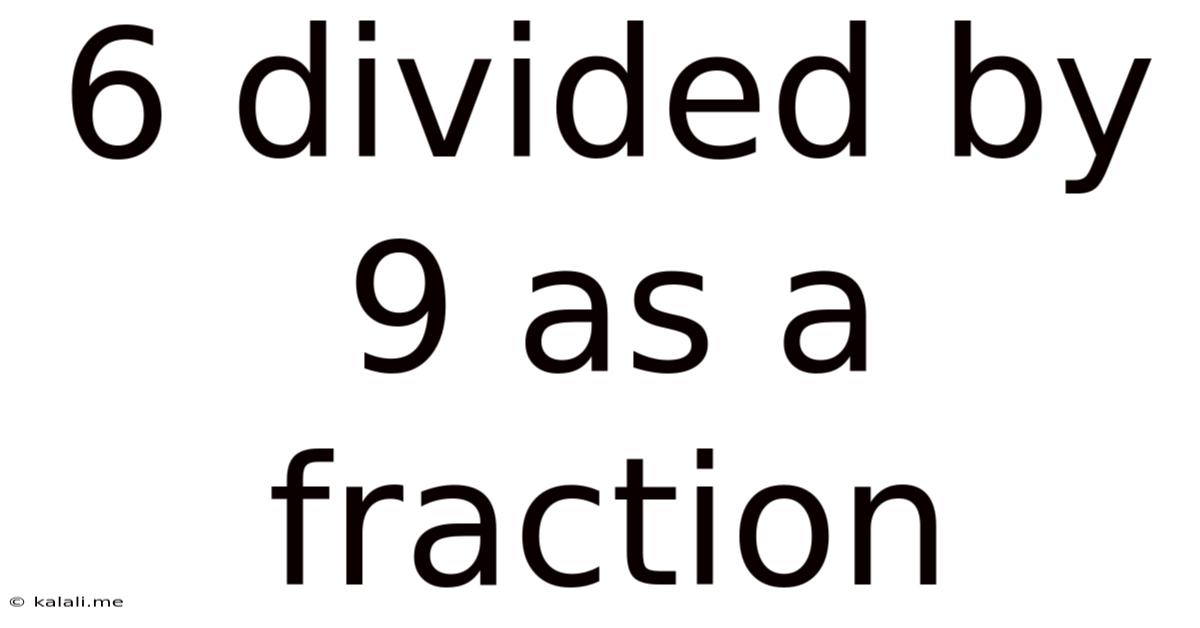
Table of Contents
6 Divided by 9 as a Fraction: A Comprehensive Guide
Meta Description: Learn how to express 6 divided by 9 as a fraction, simplifying it to its lowest terms. This guide covers the fundamental concepts of division and fractions, offering clear explanations and examples for a thorough understanding. We'll explore different methods, including using long division and simplifying fractions, ensuring you master this essential mathematical concept.
Dividing whole numbers and expressing the result as a fraction is a fundamental concept in arithmetic. This comprehensive guide will delve into the process of expressing 6 divided by 9 as a fraction, explaining the steps involved and demonstrating various methods to arrive at the simplest form of the fraction. We'll explore the underlying principles, providing a solid foundation for anyone looking to improve their understanding of fractions and division.
Understanding the Basics: Division and Fractions
Before we tackle the specific problem of 6 divided by 9, let's refresh our understanding of division and fractions.
Division: Division is the process of splitting a quantity into equal parts. For example, 12 divided by 3 (written as 12 ÷ 3 or 12/3) means splitting 12 into 3 equal groups, resulting in 4 in each group.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of equal parts the whole is divided into. For example, ½ represents one out of two equal parts.
Connecting Division and Fractions: Division and fractions are intrinsically linked. When we divide a whole number by another whole number, the result can always be expressed as a fraction. The dividend (the number being divided) becomes the numerator, and the divisor (the number we're dividing by) becomes the denominator.
Expressing 6 Divided by 9 as a Fraction
Now, let's apply these concepts to our problem: 6 divided by 9.
Following the rule above, we can directly express 6 divided by 9 as a fraction:
6 ÷ 9 = 6/9
This fraction represents six parts out of a total of nine equal parts. However, this fraction isn't in its simplest form. We can simplify it further.
Simplifying Fractions: Finding the Lowest Terms
Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. To do this, we need to find the greatest common divisor (GCD) of the numerator and denominator.
The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. For 6 and 9, the GCD is 3.
To simplify the fraction 6/9, we divide both the numerator and the denominator by the GCD:
6 ÷ 3 = 2 9 ÷ 3 = 3
Therefore, the simplified fraction is:
6/9 = 2/3
This means that 6 divided by 9 is equal to 2/3. This is the simplest form of the fraction, as 2 and 3 share no common factors other than 1.
Alternative Methods for Solving 6 Divided by 9
While the direct method is the most straightforward, let's explore alternative approaches to arrive at the same result:
1. Using Long Division:
Long division is a more traditional method for performing division. Here's how to solve 6 divided by 9 using long division:
0.666...
9 | 6.000
-0
---
60
-54
---
60
-54
---
6...
The result is a repeating decimal: 0.666... While this is a valid representation of the result, we can convert this repeating decimal back into a fraction. However, this method is less efficient than directly forming the fraction and then simplifying.
2. Prime Factorization:
Prime factorization involves breaking down numbers into their prime factors (numbers divisible only by 1 and themselves). This method can help in finding the GCD easily.
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3 x 3
The common factor is 3. Dividing both numerator and denominator by 3, we again obtain 2/3.
Understanding the Meaning of 2/3
It's important to understand the practical meaning of the fraction 2/3. It represents two parts out of three equal parts of a whole. Imagine a pizza cut into three equal slices. If you eat two slices, you have eaten 2/3 of the pizza.
Applications of Fractions in Real-World Scenarios
Fractions are used extensively in various real-world situations:
- Cooking and Baking: Recipes often require fractional amounts of ingredients (e.g., 2/3 cup of sugar).
- Measurement: Measurements often involve fractions (e.g., 1/2 inch, 3/4 yard).
- Finance: Calculating interest rates and proportions often utilizes fractions.
- Construction: Building plans and measurements frequently incorporate fractions.
- Probability: Expressing chances and likelihoods often involves fractions.
Further Exploration: Working with Fractions
This guide provides a solid foundation for understanding how to express 6 divided by 9 as a fraction and simplify it. To further enhance your understanding, consider exploring the following concepts:
- Adding and subtracting fractions: Learn how to find common denominators and perform these operations.
- Multiplying and dividing fractions: Understand the rules for multiplying and dividing fractions.
- Converting between fractions, decimals, and percentages: Learn the methods for converting between these different representations of numbers.
- Working with mixed numbers: Understand how to work with numbers that have both a whole number and a fractional part.
- Solving word problems involving fractions: Apply your understanding of fractions to solve real-world problems.
By mastering these concepts, you will build a strong foundation in arithmetic and improve your problem-solving skills. Remember to practice regularly, and don't hesitate to seek further resources if needed. The ability to work confidently with fractions is a crucial skill that extends far beyond the classroom. Understanding the relationship between division and fractions is a key building block in advanced mathematical concepts. Therefore, solidifying your understanding of this fundamental principle will greatly benefit your future mathematical endeavors. Practice makes perfect, so continue to solve similar problems and gradually increase the complexity to enhance your skill and confidence.
Latest Posts
Latest Posts
-
What Are Numbers In A Subtraction Problem Called
Aug 25, 2025
-
How Often Is Fathers Day On June 16
Aug 25, 2025
-
A Rapidly Ringing Bell Every Minute Signals What
Aug 25, 2025
-
What Does Nightcap Mean On A Warrant
Aug 25, 2025
-
How Much Is One Pound Of Pasta
Aug 25, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By 9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.