6 Is What Percent Of 30
Kalali
Apr 23, 2025 · 5 min read
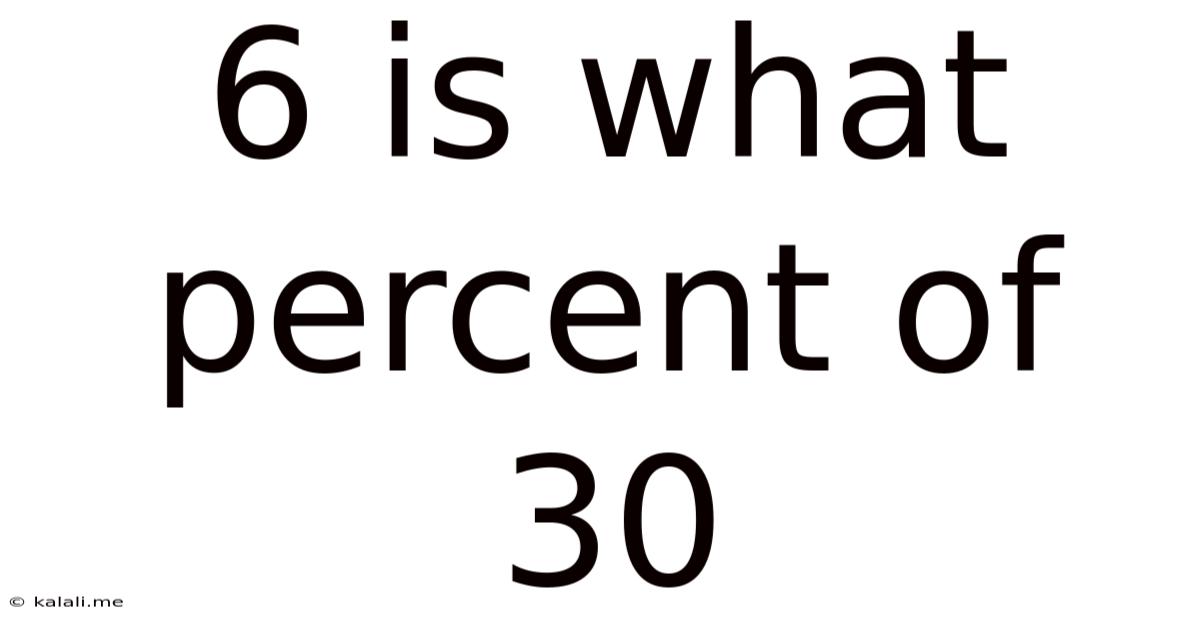
Table of Contents
6 is What Percent of 30? A Comprehensive Guide to Percentage Calculations
This seemingly simple question – "6 is what percent of 30?" – opens the door to a world of practical applications in everyday life, from calculating discounts and sales tax to understanding statistics and financial data. This comprehensive guide will not only answer the question directly but also explore the underlying concepts of percentages, providing you with the tools and knowledge to tackle similar percentage problems confidently. We'll delve into multiple methods of solving this type of problem, offering clarity and a deeper understanding of the mathematics involved. By the end, you'll be equipped to handle percentage calculations with ease and precision.
What is a Percentage?
Before diving into the solution, let's establish a clear understanding of what a percentage actually represents. A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). So, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this fundamental concept is key to mastering percentage calculations.
Method 1: Using the Percentage Formula
The most common and straightforward method for solving percentage problems involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 6 (the number we're interested in finding the percentage of)
- Whole: 30 (the total amount)
Substituting these values into the formula:
(6 / 30) * 100% = 0.2 * 100% = 20%
Therefore, 6 is 20% of 30.
Method 2: Setting up a Proportion
Another effective way to solve percentage problems is by setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion as follows:
6/30 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
30x = 600
x = 600 / 30
x = 20
Therefore, 6 is 20% of 30. This method highlights the relationship between fractions and percentages, emphasizing that a percentage is simply a fraction expressed as a number out of 100.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, we express the relationship as a fraction: 6/30
Then, we simplify the fraction: 6/30 = 1/5
Next, we convert the fraction to a decimal by dividing the numerator by the denominator: 1 ÷ 5 = 0.2
Finally, we multiply the decimal by 100 to express it as a percentage: 0.2 * 100% = 20%
This method demonstrates the interconnectedness between fractions, decimals, and percentages – all different ways of representing the same numerical value.
Real-World Applications of Percentage Calculations
Understanding percentage calculations isn't just about solving math problems; it's a crucial skill applicable to numerous real-world situations. Here are a few examples:
-
Sales and Discounts: Imagine a store offering a 20% discount on an item originally priced at $30. Using our knowledge, we can quickly calculate the discount amount: 20% of $30 is $6, resulting in a final price of $24.
-
Taxes: Sales tax is often expressed as a percentage. If the sales tax is 6%, calculating the tax on a $100 purchase is straightforward: 6% of $100 is $6.
-
Financial Calculations: Percentages are fundamental in finance, appearing in interest rates, investment returns, and profit margins. Understanding these percentages allows for informed financial decisions.
-
Statistics and Data Analysis: Percentages are used extensively to represent data and trends in various fields, including market research, scientific studies, and social sciences.
-
Grade Calculation: Calculating your final grade often involves percentage weighting of different assignments. Understanding the percentage contribution of each assignment helps you better track your overall progress.
Advanced Percentage Problems and Techniques
While the problem "6 is what percent of 30?" is relatively straightforward, understanding the underlying principles allows you to tackle more complex percentage problems. Some examples include:
-
Finding the whole when given the part and percentage: For example, if 20% of a number is 12, what is the number? This involves rearranging the percentage formula.
-
Finding the part when given the whole and percentage: For instance, what is 15% of 80? This is a direct application of the percentage formula.
-
Percentage increase and decrease: Calculating percentage changes is crucial in various applications. For example, calculating the percentage increase in sales from one year to the next.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding this is crucial for financial planning and investments.
Tips and Tricks for Mastering Percentage Calculations
-
Memorize common percentage equivalents: Knowing that 1/4 = 25%, 1/2 = 50%, and 3/4 = 75% can significantly speed up calculations.
-
Practice regularly: The more you practice, the more comfortable and confident you'll become.
-
Use different methods: Trying various methods helps build a solid understanding of the concepts and reinforces your learning.
-
Check your work: Always verify your answers to ensure accuracy.
-
Utilize online calculators (for complex problems): While understanding the underlying principles is key, online calculators can be helpful for verifying complex calculations or handling large datasets.
Conclusion: Beyond the Basics of Percentage Calculations
The seemingly simple question, "6 is what percent of 30?", serves as a gateway to a world of practical applications. Mastering percentage calculations is a valuable life skill that transcends the confines of mathematics. From everyday shopping to complex financial decisions, understanding percentages equips you with the tools to navigate the numerical landscape with confidence and accuracy. By understanding the underlying principles, practicing different methods, and applying your knowledge to real-world situations, you can transform your understanding of percentages from a basic concept to a powerful tool for problem-solving. The more you practice, the more natural and intuitive these calculations will become, allowing you to confidently tackle any percentage problem you encounter.
Latest Posts
Latest Posts
-
What Is 67 Inches In Cm
Apr 23, 2025
-
7 To The Power Of 10
Apr 23, 2025
-
Are Same Side Exterior Angles Congruent
Apr 23, 2025
-
What Is The Importance Of Crossing Over
Apr 23, 2025
-
Which Unit Is Used To Measure Force
Apr 23, 2025
Related Post
Thank you for visiting our website which covers about 6 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.