60 Is 12 Of What Number
Kalali
Apr 15, 2025 · 4 min read
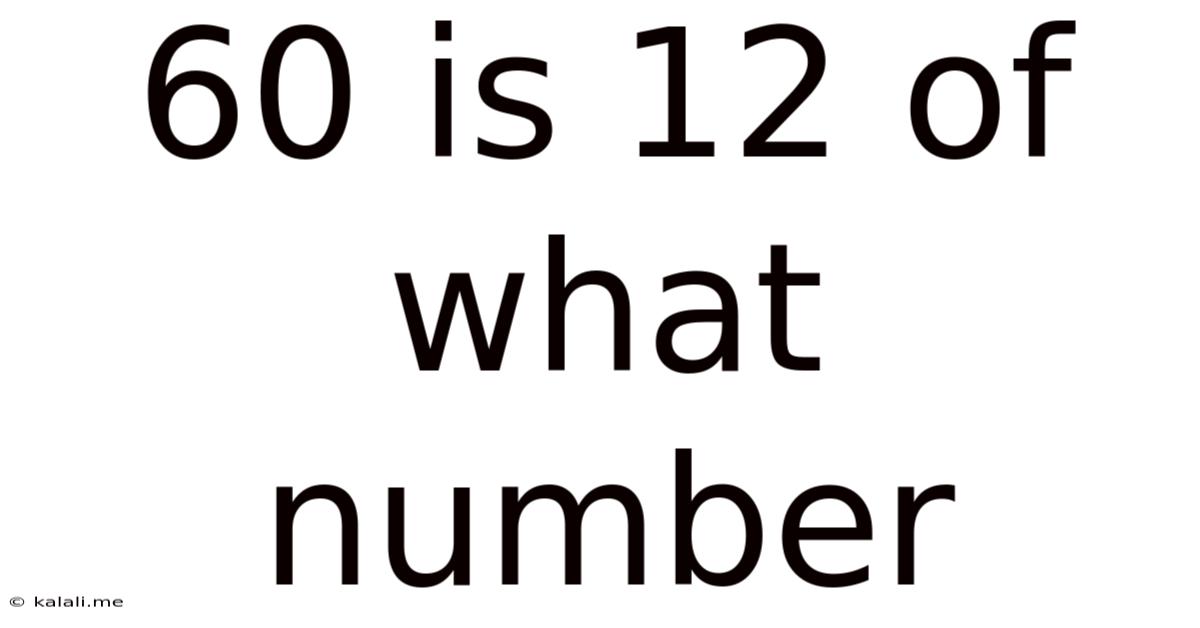
Table of Contents
60 is 12% of What Number? A Comprehensive Guide to Percentage Calculations
Finding the whole from a percentage and a part is a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating sales tax and discounts to understanding financial reports and analyzing statistical data. This article provides a comprehensive guide to solving problems like "60 is 12% of what number?", explaining the underlying principles, different solution methods, and practical examples. We'll explore various approaches, including using equations, proportions, and even mental math techniques, ensuring you master this crucial skill.
Understanding the Problem: Deconstructing Percentages
Before diving into the solutions, let's break down the problem statement: "60 is 12% of what number?" This sentence translates into a mathematical relationship where 60 represents a portion (or part) of a larger unknown number. The "12%" indicates the proportional relationship between the part (60) and the whole (the unknown number). This type of problem requires us to find the original value (the whole) from a given percentage and its corresponding part. Mastering this skill allows you to confidently handle various percentage-based calculations.
Method 1: Using an Algebraic Equation
This is the most common and arguably the most straightforward method. We can translate the problem into an algebraic equation:
- Let 'x' represent the unknown number.
- 12% can be written as 0.12 (or 12/100).
Therefore, the equation becomes:
0.12x = 60
To solve for 'x', we simply divide both sides of the equation by 0.12:
x = 60 / 0.12
x = 500
Therefore, 60 is 12% of 500.
Method 2: Using Proportions
Proportions offer an alternative and intuitive way to solve percentage problems. We can set up a proportion using the given information:
- Part/Whole = Percentage/100
Substituting the known values:
60/x = 12/100
To solve for 'x', we can cross-multiply:
60 * 100 = 12 * x
6000 = 12x
x = 6000 / 12
x = 500
Again, we find that 60 is 12% of 500. This method highlights the relationship between the parts and the whole in a clear and visual manner.
Method 3: Using the Percentage Formula
The basic percentage formula is:
(Part/Whole) * 100 = Percentage
We can rearrange this formula to solve for the whole:
Whole = (Part * 100) / Percentage
Plugging in the values from our problem:
Whole = (60 * 100) / 12
Whole = 6000 / 12
Whole = 500
Once more, we confirm that 60 is 12% of 500. This method offers a concise and direct approach to solving the problem.
Method 4: Mental Math Techniques (for simpler percentages)
While less practical for complex percentages, mental math can be surprisingly effective for simpler scenarios. Recognizing that 12% is 1/8th (12.5% would be closer, but we can approximate for this), we can approach it like this:
If 12% is approximately 1/8th of the total, then 60 represents 1/8th of the unknown number. Therefore, the total number would be 8 times 60:
8 * 60 = 480
This is an approximation, as we used 12% ≈ 1/8. The result isn't 500 precisely due to this rounding, but it provides a quick estimate. This method is helpful for developing intuition and making quick estimations.
Practical Applications and Real-World Examples
Understanding how to calculate the whole from a percentage and a part is crucial in numerous real-world situations:
- Sales and Discounts: If a discounted item costs $60 after a 12% discount, you can calculate the original price using the methods described above.
- Financial Analysis: Determining the total investment amount given a percentage return and profit amount.
- Statistical Data Analysis: Calculating the total population from a sample percentage and the sample size.
- Tax Calculations: Finding the pre-tax amount given the tax amount and tax rate.
- Business Projections: Estimating total sales based on a percentage of achieved targets.
- Scientific Experiments: Determining the total sample size based on the number of successful results and the success rate.
Expanding the Concept: Variations and Extensions
The core principle discussed here – finding the whole from a given percentage and its part – is a foundation for solving more complex percentage problems. Variations might include:
- Multiple percentages: Calculating the original price after multiple successive discounts or markups. This involves applying the percentage calculations sequentially.
- Compound interest: Calculating the principal amount given the interest earned over a period of time. This incorporates the concept of exponential growth.
- Inverse percentages: Determining the percentage change between two values. This involves using ratios and differences.
Troubleshooting Common Mistakes
- Incorrect conversion of percentages to decimals: Always remember to convert percentages to their decimal equivalents (e.g., 12% = 0.12) before using them in calculations.
- Incorrect equation setup: Double-check that your equation correctly represents the relationship between the part, the whole, and the percentage.
- Calculation errors: Carefully review your calculations to avoid simple arithmetic mistakes.
Conclusion: Mastering Percentage Calculations
The ability to calculate the whole from a part and a percentage is a valuable skill with broad applications. Understanding the different methods – algebraic equations, proportions, and the percentage formula – empowers you to solve various percentage-related problems confidently. By mastering this fundamental concept, you can improve your problem-solving abilities and navigate numerous real-world scenarios that involve percentages. Remember to practice regularly, applying these techniques to diverse problems to reinforce your understanding and build your confidence in tackling percentage calculations. The more you practice, the more intuitive and efficient your approach will become.
Latest Posts
Latest Posts
-
How Many Inches Is A Meter Stick
Jul 10, 2025
-
Soundtrack To Step Up 2 The Streets
Jul 10, 2025
-
Keebler Club And Cheddar Crackers Expiration Date
Jul 10, 2025
-
In Many States Trailers With A Gvwr Of 1500
Jul 10, 2025
-
How Many Tablespoons Are In A Hidden Valley Ranch Packet
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 12 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.