60 Is 15 Of What Number
Kalali
Apr 10, 2025 · 5 min read
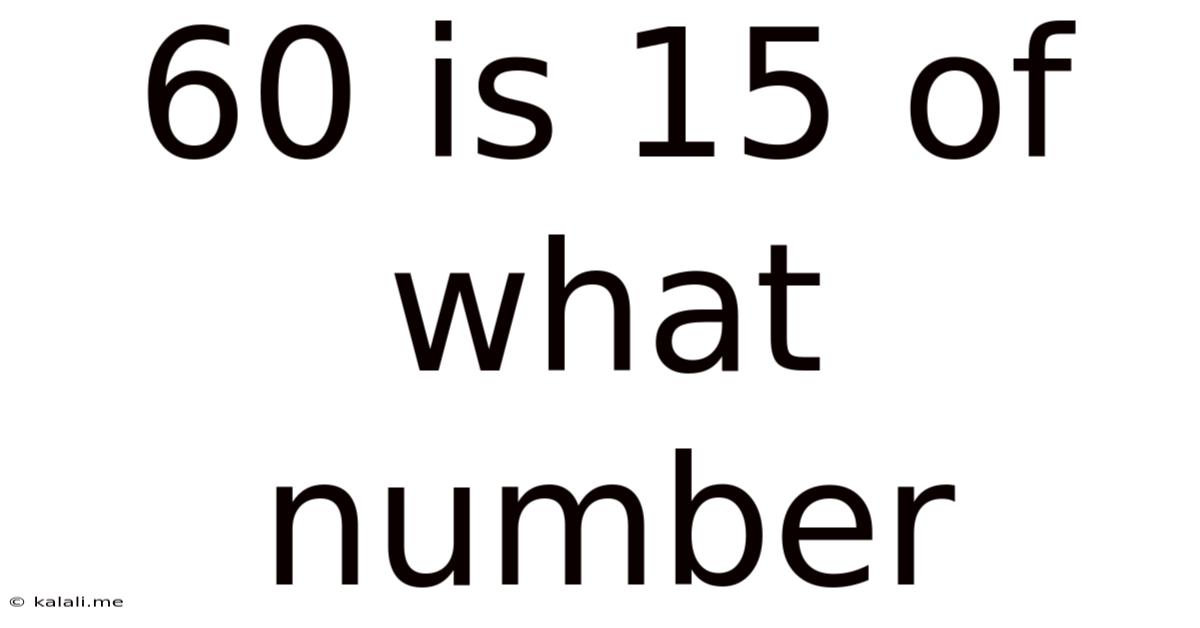
Table of Contents
60 is 15% of What Number? A Comprehensive Guide to Percentage Calculations
This article delves deep into the question: "60 is 15% of what number?" We'll not only provide the answer but also explore the underlying mathematical principles, various solution methods, and practical applications of percentage calculations. Understanding percentages is crucial in numerous aspects of life, from finance and shopping to data analysis and scientific research. This guide will empower you to confidently tackle percentage problems of all complexities.
Meta Description: Learn how to solve "60 is 15% of what number?" We explore multiple methods, including algebraic equations and proportion techniques, and demonstrate their practical applications in various scenarios.
Understanding Percentages
Before diving into the solution, let's solidify our understanding of percentages. A percentage is a fraction expressed as a part of 100. The symbol "%" represents "per hundred." For instance, 15% means 15 out of 100, which can be written as the fraction 15/100 or the decimal 0.15. This fundamental understanding forms the basis for all percentage calculations.
Method 1: Using Algebraic Equations
This is the most common and arguably the most straightforward method for solving percentage problems. We can translate the problem "60 is 15% of what number" into an algebraic equation:
60 = 0.15 * x
Where:
- 60 represents the given value.
- 0.15 represents 15% (converted to decimal form).
- x represents the unknown number we are trying to find.
To solve for x, we perform the following steps:
-
Divide both sides of the equation by 0.15: This isolates x on one side of the equation.
60 / 0.15 = x
-
Calculate the result:
x = 400
Therefore, 60 is 15% of 400.
Method 2: Using Proportions
Proportions offer an alternative approach to solving percentage problems. A proportion is a statement that two ratios are equal. We can set up a proportion based on the given information:
15/100 = 60/x
This proportion states that the ratio of 15 to 100 is equal to the ratio of 60 to the unknown number (x).
To solve for x, we can use cross-multiplication:
15 * x = 100 * 60
15x = 6000
Now, divide both sides by 15:
x = 6000 / 15
x = 400
Again, we arrive at the solution: 60 is 15% of 400.
Method 3: Using the Percentage Formula
The basic percentage formula can be expressed as:
(Part / Whole) * 100 = Percentage
In our problem, we know the part (60) and the percentage (15%). We need to find the whole. We can rearrange the formula to solve for the whole:
Whole = (Part / Percentage) * 100
Substituting the known values:
Whole = (60 / 15) * 100
Whole = 4 * 100
Whole = 400
This method confirms once more that 60 is 15% of 400.
Practical Applications of Percentage Calculations
Understanding percentage calculations is invaluable in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, determining the final price of an item after a 20% discount or calculating the total cost including sales tax involves percentage calculations.
-
Shopping: Comparing prices, evaluating discounts, and understanding unit costs require an understanding of percentages. For example, figuring out which deal is better—a 15% discount or a $10 discount—involves calculating the final price based on each offer.
-
Data Analysis: Percentages are frequently used to represent proportions and trends in data. Graphs and charts often utilize percentages to illustrate proportions within datasets. This is crucial in fields like market research and scientific studies.
-
Science: Percentage calculations are used extensively in various scientific fields, such as chemistry (concentration of solutions), biology (population growth), and physics (efficiency of machines).
-
Everyday Life: Calculating tips in restaurants, understanding statistics presented in news reports, and even interpreting survey results often involve working with percentages.
Advanced Percentage Problems
While the problem "60 is 15% of what number?" is relatively straightforward, the principles involved can be applied to more complex scenarios. For instance:
-
Finding the percentage increase or decrease: Calculating the percentage change between two values requires understanding how to determine the difference and express it as a percentage of the original value.
-
Compound interest calculations: Compound interest involves calculating interest on both the principal amount and accumulated interest. This requires repeated percentage calculations.
-
Solving problems involving multiple percentages: Scenarios involving successive discounts or multiple tax rates require a clear understanding of how to combine percentages correctly.
Tips for Solving Percentage Problems
Here are some helpful tips to enhance your ability to tackle percentage problems:
-
Convert percentages to decimals: Converting percentages to decimals (e.g., 15% to 0.15) simplifies calculations significantly.
-
Use a consistent method: Choose a method (algebraic equations, proportions, or the percentage formula) that you understand well and stick with it for consistency.
-
Check your work: Always double-check your calculations to ensure accuracy. Using a calculator can help minimize errors.
-
Practice regularly: The more you practice solving percentage problems, the more comfortable and proficient you will become.
Conclusion
This article has provided a comprehensive exploration of how to solve the problem "60 is 15% of what number?". We explored three different methods – using algebraic equations, proportions, and the percentage formula – demonstrating their equivalence and versatility. We also highlighted the numerous practical applications of percentage calculations in various fields and offered tips for solving percentage problems effectively. By mastering these techniques, you'll be well-equipped to confidently tackle a wide range of percentage-related challenges in your personal and professional life. Remember that consistent practice is key to mastering percentage calculations and developing a strong mathematical foundation.
Latest Posts
Latest Posts
-
Is Burning Physical Or Chemical Change
Apr 18, 2025
-
How Big Is 80 Inches In Feet
Apr 18, 2025
-
What Is 56 As A Fraction
Apr 18, 2025
-
How Many Cups Equal 48 Ounces
Apr 18, 2025
-
110 Cm Equals How Many Inches
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 15 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.