60 Is What Percent Of 25
Kalali
Apr 15, 2025 · 5 min read
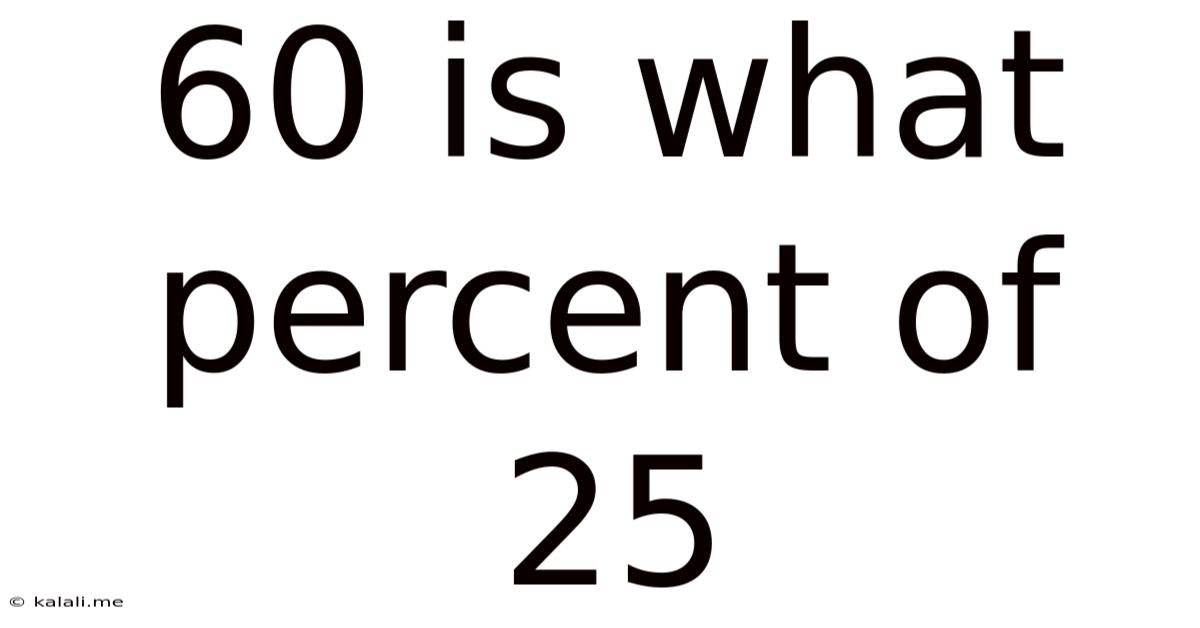
Table of Contents
60 is What Percent of 25? Understanding Percentages and Their Applications
This seemingly simple question, "60 is what percent of 25?", opens the door to a broader understanding of percentages, their calculations, and their wide-ranging applications in various fields. While the answer itself is straightforward, exploring the underlying concepts and practical uses enriches our mathematical literacy and problem-solving skills. This article will delve into the solution, explaining the process step-by-step and then expanding on the significance of percentages in everyday life and professional contexts.
Meta Description: Learn how to calculate percentages easily! This comprehensive guide explains how to determine what percentage 60 represents of 25, providing step-by-step calculations and exploring real-world applications of percentage calculations.
Solving the Problem: 60 is What Percent of 25?
At first glance, it might seem counterintuitive that 60 can be a percentage of a smaller number like 25. This is because percentages represent parts of a whole, and the "whole" can be less than the "part" in certain scenarios. Let's break down the calculation:
To find what percent 60 is of 25, we'll use the following formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 60
- Whole: 25
Substituting these values into the formula:
(60 / 25) * 100 = 240%
Therefore, 60 is 240% of 25.
Understanding the Result: Percentages Greater Than 100%
The result of 240% might seem unusual at first. We are used to percentages ranging from 0% to 100%, representing portions of a whole. However, percentages can indeed exceed 100%. This signifies that the "part" is larger than the "whole." Think of it like this: you have 25 apples (the whole), and somehow you now have 60 apples (the part). You have more than 100% of your original amount. The extra apples came from somewhere else, exceeding the initial quantity.
Practical Applications of Percentage Calculations: Beyond the Basics
Understanding percentage calculations goes far beyond simple mathematical exercises. They are fundamental tools used across numerous disciplines, including:
-
Finance: Interest rates, loan calculations, investment returns, and tax calculations all heavily rely on percentages. For example, understanding compound interest requires a firm grasp of percentage growth over time. Calculating discounts and markups in retail pricing also depends heavily on percentage calculations. Analyzing financial statements often involves comparing figures as percentages of the total, such as revenue growth, profit margins, and debt-to-equity ratios.
-
Science: Many scientific experiments and data analysis involve percentages. Expressing experimental results, calculating error margins, and analyzing statistical data often uses percentages to represent proportions and relationships. For instance, a scientist might report that 75% of participants in a study showed a particular response.
-
Business: Profit margins, market share calculations, sales growth rates, and cost-benefit analyses are all critically reliant on accurate percentage calculations. Business decisions are often guided by the analysis of key performance indicators (KPIs), expressed as percentages to show relative performance improvements or declines. For example, a company might track its customer retention rate as a percentage to assess its customer loyalty.
-
Everyday Life: Percentages are integral to everyday life, from calculating tips at restaurants (e.g., a 15% tip) and understanding sales discounts (e.g., 20% off) to comprehending interest rates on credit cards and loans. Calculating your savings rate and understanding your tax bracket both involve working with percentages.
Advanced Percentage Calculations and Related Concepts
While the basic formula for calculating percentages is straightforward, there are more complex scenarios that require a deeper understanding:
-
Calculating Percentage Change: This involves determining the percentage increase or decrease between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100. This is crucial for understanding growth or decline in various metrics, such as stock prices, population numbers, or sales figures. For instance, if sales increased from 100 units to 120 units, the percentage change is [(120 - 100) / 100] * 100 = 20%. -
Calculating Percentage Increase/Decrease from a Given Percentage: If a value is increased or decreased by a certain percentage, the resulting value can be calculated using the following formula:
Original Value * (1 + Percentage Increase/Decrease). For example, increasing a value by 10% is equivalent to multiplying the original value by 1.10 (1 + 0.10). Conversely, decreasing a value by 10% involves multiplying the original value by 0.90 (1 - 0.10). -
Working with Multiple Percentages: In scenarios where multiple percentages are involved (e.g., successive discounts or compounded interest), it's essential to apply the percentages sequentially and avoid simply adding them together. This is because each percentage is applied to a different base value.
-
Reverse Percentage Calculations: Sometimes you need to find the original value given the final value and the percentage change. These calculations involve working backward using the same principles, often requiring algebraic manipulation.
Real-World Examples of Percentage Applications
Here are some concrete examples illustrating the diverse applications of percentage calculations:
-
A store offers a 30% discount on a $100 item. What is the final price?
- Discount amount: $100 * 0.30 = $30
- Final price: $100 - $30 = $70
-
A company's revenue increased from $50,000 to $60,000. What is the percentage increase?
- Percentage increase: [(60,000 - 50,000) / 50,000] * 100 = 20%
-
A student scored 80 out of 100 on a test. What is their percentage score?
- Percentage score: (80 / 100) * 100 = 80%
-
An investment grows by 10% per year for three years. What is the total percentage increase over the three years? (Note: this requires compound interest calculations.)
-
A survey revealed that 65% of respondents prefer a particular brand. If 500 people participated in the survey, how many people prefer that brand?
- Number of people: 500 * 0.65 = 325
Conclusion: Mastering Percentages for Success
Understanding percentages is a fundamental skill with far-reaching implications across various aspects of life. Whether dealing with financial matters, interpreting scientific data, making business decisions, or simply navigating everyday situations, a strong grasp of percentage calculations enables informed choices and accurate analyses. While the core concept is relatively simple, exploring advanced applications and related concepts strengthens problem-solving abilities and enhances mathematical fluency. Mastering percentages empowers you to confidently tackle numerical challenges and make sound judgments based on quantitative information. By understanding the intricacies of percentage calculations and their broad applications, you unlock a powerful tool for navigating the complexities of the world around you.
Latest Posts
Latest Posts
-
How Many Square Yards In One Acre
Jul 02, 2025
-
What Is 2 3 Of 3 Quarts
Jul 02, 2025
-
Courtesy Is Cumbersome To Them That Know It Not
Jul 02, 2025
-
How Far Is 220 Yards On A Track
Jul 02, 2025
-
What Is The Shortest Chapter In The Bible
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about 60 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.