60 Is What Percent Of 80
Kalali
Apr 10, 2025 · 5 min read
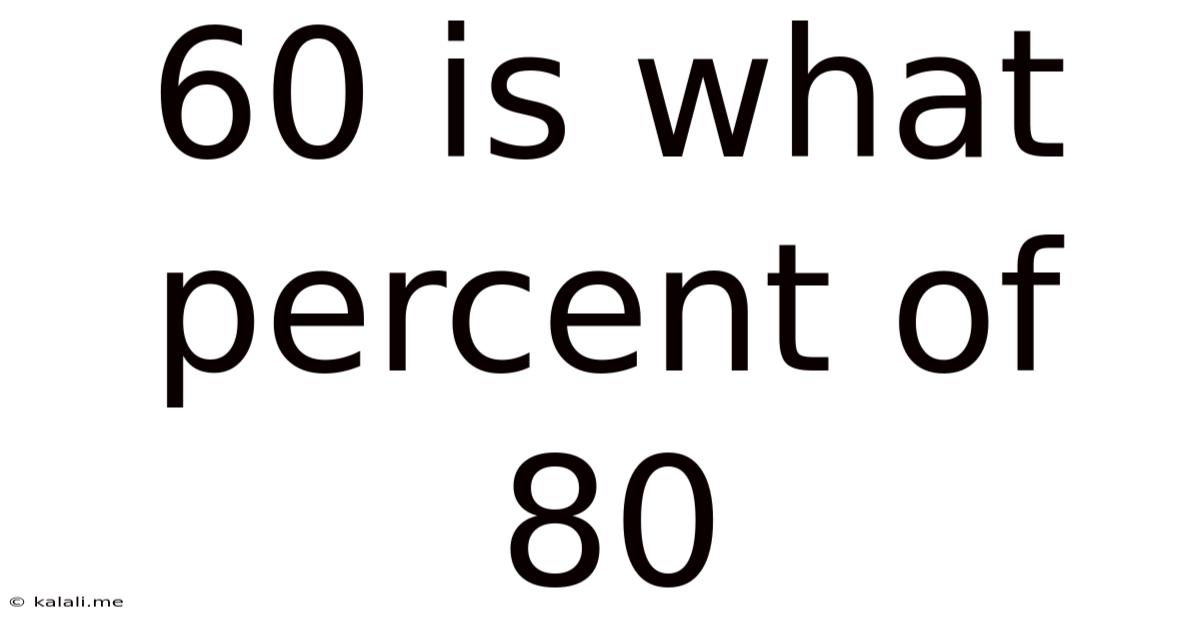
Table of Contents
60 is What Percent of 80? A Deep Dive into Percentage Calculations and Real-World Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analyses and scientific research. This article will thoroughly explore how to determine what percentage 60 represents of 80, explaining the underlying mathematical concepts and illustrating its practical relevance through diverse examples. We'll also delve into different methods of solving percentage problems, equipping you with a comprehensive understanding of this crucial mathematical concept.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "60 is what percent of 80?". This guide covers various methods, real-world applications, and practical tips for mastering percentage calculations.
Understanding the Fundamentals of Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Percentages provide a standardized way to compare proportions and express parts of a whole. They are invaluable tools for representing data, making comparisons, and understanding proportions across different scales.
Before tackling the specific problem of "60 is what percent of 80?", let's refresh the basic formula for calculating percentages:
(Part / Whole) * 100% = Percentage
In this formula:
- Part: Represents the specific portion you're interested in expressing as a percentage.
- Whole: Represents the total amount or the complete entity.
- Percentage: The result expressed as a number followed by the "%" symbol.
Method 1: Using the Basic Percentage Formula
To find out what percentage 60 is of 80, we'll substitute the values into our formula:
(60 / 80) * 100% = Percentage
First, we perform the division:
60 / 80 = 0.75
Then, we multiply the result by 100%:
0.75 * 100% = 75%
Therefore, 60 is 75% of 80.
Method 2: Using Proportions
Another effective approach to solving percentage problems involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
60/80 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
60 * 100 = 80 * x
6000 = 80x
Now, we solve for 'x' by dividing both sides by 80:
x = 6000 / 80
x = 75
Therefore, x = 75%, confirming our previous result.
Method 3: Using Decimal Conversion
We can also approach this problem by first converting the fraction 60/80 into a decimal and then multiplying by 100%.
60/80 = 0.75
0.75 * 100% = 75%
This method highlights the direct relationship between decimals and percentages. Multiplying a decimal by 100% effectively shifts the decimal point two places to the right, resulting in the percentage value.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is incredibly versatile and finds applications in numerous contexts:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding how much interest you'll accrue on a savings account or how much you'll save with a sale discount requires proficiency in percentages. A 20% discount on a $100 item would save you $20 (20% of $100).
-
Business and Economics: Analyzing market share, growth rates, inflation, and unemployment statistics often involves interpreting and comparing percentages. Businesses use percentages to track key performance indicators (KPIs), measure customer satisfaction, and project future sales.
-
Science and Research: Percentages are widely used in scientific research to represent experimental results, statistical data, and error margins. For instance, a scientist might report that 75% of participants in a study showed a positive response to a new treatment.
-
Everyday Life: Calculating tips in restaurants, figuring out sale prices, determining the nutritional value of food (e.g., percentage of daily value of vitamins), and understanding statistics presented in news reports all utilize percentage calculations. Knowing how much tip to leave (e.g., 15% or 20% of the bill) is a common application.
-
Education: Grading systems, test scores, and performance evaluations often use percentages to represent a student's achievement. A score of 85% on an exam indicates a strong performance.
Solving More Complex Percentage Problems
While the "60 is what percent of 80?" problem is relatively straightforward, the underlying principles can be applied to more complex scenarios. For example:
-
Finding the whole: If you know that 30% of a number is 60, you can set up the equation: 0.30 * x = 60. Solving for x, you find the whole number is 200.
-
Finding the part: If you know that 25% of 120 is a certain number, you can calculate the part by multiplying 120 by 0.25, resulting in 30.
-
Percentage change: Calculating percentage increase or decrease requires considering the initial value and the change in value. For instance, if a price increases from $50 to $60, the percentage increase is calculated as: [(60-50)/50] * 100% = 20%.
Mastering these variations ensures you can tackle a wide range of percentage-related problems efficiently.
Tips for Mastering Percentage Calculations
Here are some valuable tips to improve your skills in calculating percentages:
-
Practice regularly: The more you practice, the more comfortable you'll become with the concepts and formulas. Try solving various percentage problems from different contexts.
-
Use different methods: Experiment with the different methods discussed in this article to find the approach that best suits your understanding and preference.
-
Utilize online resources: There are numerous online calculators and tutorials available to assist you with percentage calculations. These resources can be especially helpful when dealing with more complex problems.
-
Check your work: Always double-check your calculations to ensure accuracy. Small errors can significantly impact the results, especially in financial or scientific contexts.
-
Understand the context: Pay close attention to the wording of percentage problems to accurately identify the part and the whole. Misinterpreting the problem can lead to incorrect answers.
Conclusion
Calculating percentages is an essential skill applicable in numerous aspects of life. Understanding the underlying principles and practicing different methods will enhance your proficiency and enable you to solve a wide variety of percentage-related problems with confidence. Remember, the core formula (Part / Whole) * 100% = Percentage serves as the foundation for all percentage calculations. Whether you're calculating discounts, interest rates, or analyzing statistical data, a strong grasp of percentages is an invaluable asset. By mastering this fundamental mathematical concept, you equip yourself with a powerful tool for tackling everyday challenges and understanding the world around you more effectively.
Latest Posts
Latest Posts
-
How Many 32 Oz Make A Gallon
Jul 12, 2025
-
700 Is 10 Times As Much As
Jul 12, 2025
-
How Much Is 120 Kilograms In Pounds
Jul 12, 2025
-
Born In 1990 How Old Am I
Jul 12, 2025
-
What Is The Average Iq For A 5 Year Old
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about 60 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.