68 Out Of 80 As A Percentage
Kalali
Aug 21, 2025 · 5 min read
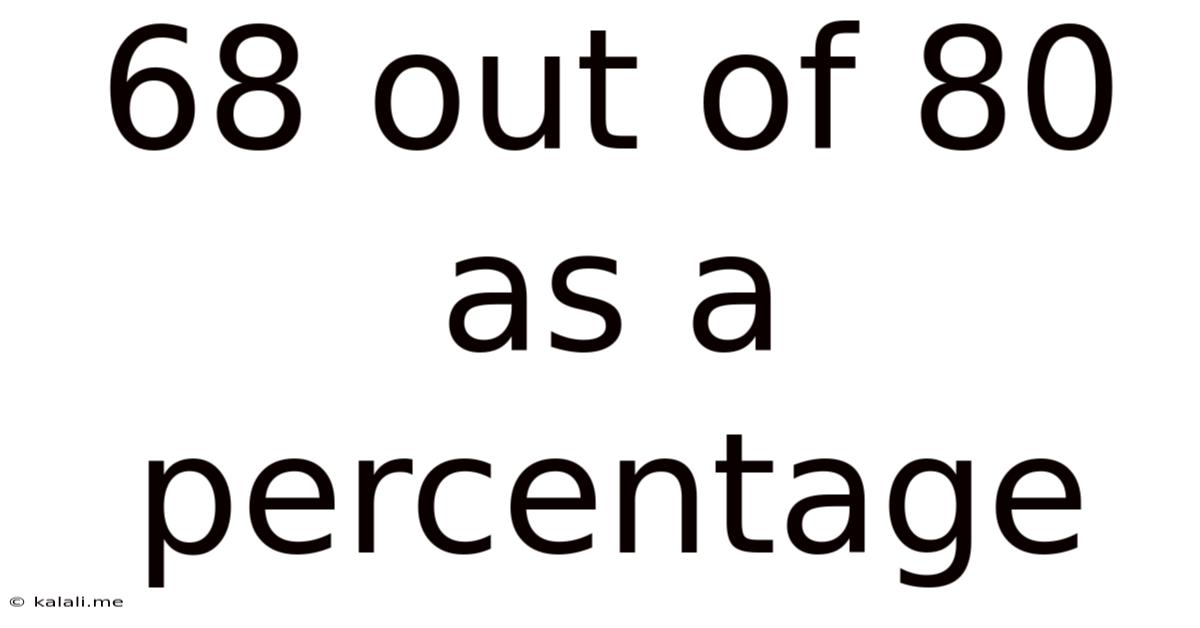
Table of Contents
68 out of 80 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from academic assessments to financial analyses. Understanding how to convert fractions into percentages is crucial for interpreting data and making informed decisions. This article will delve into calculating 68 out of 80 as a percentage, providing a step-by-step guide and exploring broader applications of percentage calculations. We'll also touch upon related concepts and offer tips for accurate and efficient calculations. This detailed explanation ensures you not only understand the solution but also grasp the underlying principles, making you confident in tackling similar percentage problems in the future.
Understanding Percentages: A Quick Refresher
Before diving into the specific calculation, let's briefly review the concept of percentages. A percentage represents a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 68 out of 80 as a Percentage: The Step-by-Step Method
To calculate 68 out of 80 as a percentage, we follow these simple steps:
-
Express the values as a fraction: The problem can be written as the fraction 68/80. This fraction represents the portion of 80 that 68 constitutes.
-
Convert the fraction to a decimal: Divide the numerator (68) by the denominator (80): 68 ÷ 80 = 0.85
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.85 × 100 = 85%
Therefore, 68 out of 80 is equal to 85%.
Alternative Calculation Methods
While the above method is straightforward, there are other approaches to arrive at the same result:
-
Using Proportions: We can set up a proportion: x/100 = 68/80. Solving for x (the percentage) involves cross-multiplication: 80x = 6800. Dividing both sides by 80 gives x = 85. Therefore, 68 out of 80 is 85%.
-
Using a Calculator: Most calculators have a percentage function. Simply enter 68 ÷ 80 and then multiply by 100 to obtain the percentage. This method offers speed and convenience, especially for more complex calculations.
Practical Applications of Percentage Calculations
The ability to calculate percentages has far-reaching applications in numerous areas:
-
Academic Performance: Calculating grades, test scores, and overall academic standing often involves percentage calculations. For example, a student scoring 68 out of 80 on a test achieved an 85%, a good understanding of the material.
-
Financial Management: Percentages are essential in various financial applications, including calculating interest rates, discounts, tax rates, profit margins, and investment returns. Understanding these percentages is crucial for making informed financial decisions. A 5% increase in salary, for instance, is easily calculated using percentage methods.
-
Data Analysis and Interpretation: Percentages are widely used to represent data in charts, graphs, and reports. This enables easy comparison and visualization of proportions within datasets. Understanding percentage changes allows for a clearer picture of trends and patterns.
-
Sales and Marketing: Sales figures, conversion rates, customer satisfaction scores, and market share are often expressed as percentages. Businesses use these percentages to track performance, identify trends, and make strategic decisions. For example, a 10% increase in sales compared to the previous year signifies positive growth.
-
Science and Engineering: Percentage calculations are used to express error margins, efficiency levels, and various measurements in scientific and engineering contexts. Precision in these calculations is paramount for accurate results and reliability.
Advanced Percentage Calculations: Beyond the Basics
While calculating 68 out of 80 is relatively straightforward, other percentage calculations can be more complex:
-
Percentage Increase/Decrease: Calculating the percentage change between two values requires subtracting the initial value from the final value, dividing the result by the initial value, and multiplying by 100. For example, if a price increases from $80 to $85, the percentage increase is ((85-80)/80) * 100 = 6.25%.
-
Percentage of a Number: Finding a percentage of a specific number involves multiplying the number by the percentage (expressed as a decimal). For example, 20% of 150 is 150 * 0.20 = 30.
-
Finding the Original Value: If you know the final value after a percentage increase or decrease, you can work backward to find the original value using algebraic techniques.
Tips for Accurate Percentage Calculations
-
Double-check your work: Always verify your calculations to avoid errors. Using a calculator can minimize manual calculation mistakes.
-
Understand the context: Ensure you correctly identify the relevant values for the calculation. Clarify whether you are calculating a percentage increase, decrease, or a simple proportion.
-
Use appropriate rounding: Round off your answers to a suitable number of decimal places based on the context of the problem. Excessive decimal places might not be necessary or meaningful.
-
Practice regularly: The more you practice percentage calculations, the more comfortable and confident you'll become. Start with simple problems and gradually move to more complex scenarios.
Conclusion
Calculating 68 out of 80 as a percentage results in 85%. This seemingly simple calculation underlines a fundamental concept with broad applications across various fields. Mastering percentage calculations is not only crucial for academic success but also for navigating the complexities of finance, data analysis, and numerous other real-world scenarios. By understanding the different methods and practicing regularly, you can confidently tackle any percentage problem and interpret data effectively. This skill empowers you to make informed decisions and analyze information accurately, enhancing your problem-solving abilities in both personal and professional spheres. Remember the importance of accuracy and double-checking your work to ensure reliability in your results.
Latest Posts
Latest Posts
-
Cities In Italy That Start With S
Aug 21, 2025
-
7 5 Dozen Eggs Is How Many Eggs
Aug 21, 2025
-
What Side Ear Is The Gay Side
Aug 21, 2025
-
How Many Teaspoons In A Gram Of Yeast
Aug 21, 2025
-
1 Pound Of Elbow Macaroni How Many Cups
Aug 21, 2025
Related Post
Thank you for visiting our website which covers about 68 Out Of 80 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.