7 Is 25 Of What Number
Kalali
Apr 24, 2025 · 5 min read
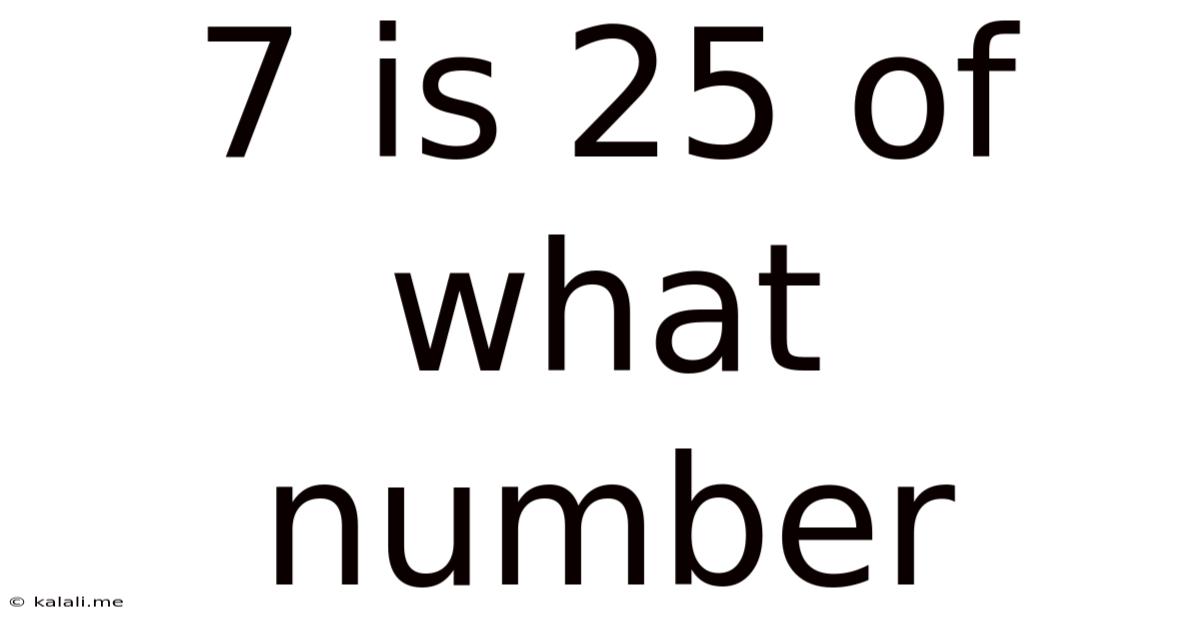
Table of Contents
7 is 25% of What Number? Unlocking the Power of Percentage Calculations
This seemingly simple question, "7 is 25% of what number?", opens the door to a world of practical applications involving percentages. Understanding how to solve this type of problem is crucial for various aspects of life, from budgeting and finance to calculating discounts and understanding statistical data. This comprehensive guide will not only show you how to solve this specific problem but also equip you with the knowledge and strategies to tackle similar percentage calculations confidently. We'll explore different methods, discuss the underlying mathematical principles, and provide real-world examples to solidify your understanding. This article is designed to be both informative and practical, offering a deep dive into the world of percentages.
Understanding Percentages: A Foundation for Success
Before diving into the solution, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." Therefore, 25% can be expressed as a fraction (25/100) or as a decimal (0.25). This conversion between percentages, fractions, and decimals is crucial for solving percentage problems efficiently.
Method 1: Using the Percentage Formula
The most straightforward way to solve "7 is 25% of what number?" is to use the basic percentage formula:
Part = Percentage × Whole
In this equation:
- Part represents the given value (7 in our case).
- Percentage represents the percentage given (25% or 0.25).
- Whole represents the unknown value we need to find.
To solve for the "Whole," we rearrange the formula:
Whole = Part / Percentage
Substituting the known values:
Whole = 7 / 0.25 = 28
Therefore, 7 is 25% of 28.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
7 / x = 25 / 100
Where 'x' represents the unknown number.
To solve this proportion, we can cross-multiply:
7 × 100 = 25 × x
700 = 25x
Now, divide both sides by 25 to isolate 'x':
x = 700 / 25 = 28
Again, we find that 7 is 25% of 28.
Method 3: Working with Decimals
Since 25% is equivalent to 0.25, we can directly translate the problem into a simple equation:
0.25x = 7
To solve for 'x', divide both sides by 0.25:
x = 7 / 0.25 = 28
This method emphasizes the direct relationship between percentages and their decimal equivalents, providing a quick and efficient solution.
Real-World Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple mathematical exercises. Consider these real-world scenarios:
-
Sales and Discounts: A store offers a 25% discount on an item priced at $28. Using the percentage formula, you can easily calculate the discount amount ($7) and the final price ($21).
-
Financial Calculations: Calculating interest on loans, investments, and savings accounts heavily relies on percentage calculations.
-
Taxation: Determining sales tax, income tax, or property tax often involves calculating percentages of income or purchase amounts.
-
Data Analysis: Percentages are essential for interpreting statistical data, such as survey results, market trends, or scientific findings. Understanding percentages allows for a more nuanced interpretation of data, identifying key trends and insights.
-
Recipe Scaling: When baking or cooking, adjusting ingredient amounts based on percentage changes is common. Doubling a recipe might involve multiplying all ingredients by 100%. Reducing a recipe might involve dividing by a percentage.
-
Tip Calculation: Calculating a tip in a restaurant often involves finding a percentage of the bill.
Expanding Your Understanding: Tackling More Complex Percentage Problems
While the problem "7 is 25% of what number?" provides a fundamental understanding of percentage calculations, let's explore some more complex scenarios:
-
Finding the Percentage Increase or Decrease: If a value increases from 20 to 25, what is the percentage increase? First, find the difference (25 - 20 = 5). Then, divide the difference by the original value (5/20 = 0.25) and multiply by 100 to get the percentage increase (25%).
-
Calculating Percentage Change with Negative Values: Handling negative percentage changes involves similar steps but requires careful attention to signs. A decrease from 50 to 40 represents a 20% decrease ((10/50)*100).
-
Solving Problems with Multiple Percentages: Scenarios involving consecutive percentage changes, such as discounts applied sequentially, require careful step-by-step calculations. For example, a 10% discount followed by a 5% discount on the reduced price is not the same as a 15% discount.
-
Dealing with Compound Interest: Compound interest calculations involve applying a percentage repeatedly over time, resulting in exponential growth.
Mastering Percentage Calculations: Tips and Strategies
To become proficient in solving percentage problems, consider these strategies:
-
Familiarize yourself with the percentage formula: Understanding the relationship between the part, the percentage, and the whole is paramount.
-
Practice regularly: The more you practice, the more comfortable and confident you will become.
-
Use different methods: Experiment with different approaches to find the method that best suits your understanding and preferences.
-
Check your work: Always verify your calculations to ensure accuracy.
-
Utilize online resources: Numerous online calculators and tutorials can assist you in learning and practicing percentage calculations.
Conclusion: Beyond the Basics of Percentages
The seemingly simple question, "7 is 25% of what number?" serves as a gateway to understanding the broader world of percentage calculations. By mastering these fundamental concepts and applying the methods discussed, you’ll be well-equipped to handle a wide range of practical applications in various aspects of life. Remember that consistent practice and exploration of different problem types will solidify your understanding and build your confidence in tackling even the most challenging percentage-related calculations. The ability to confidently work with percentages is a valuable skill that will serve you well throughout your academic and professional pursuits.
Latest Posts
Latest Posts
-
Which Career Combines Dna Technology And Medicine
Apr 24, 2025
-
59 Inches Is How Many Centimeters
Apr 24, 2025
-
32 Centimeters Equals How Many Inches
Apr 24, 2025
-
How Many Atp Are Created By Fermentation
Apr 24, 2025
-
21 Degrees C Is What In Fahrenheit
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about 7 Is 25 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.