7 Is To 34 As 5 Is To
Kalali
Jun 30, 2025 · 6 min read
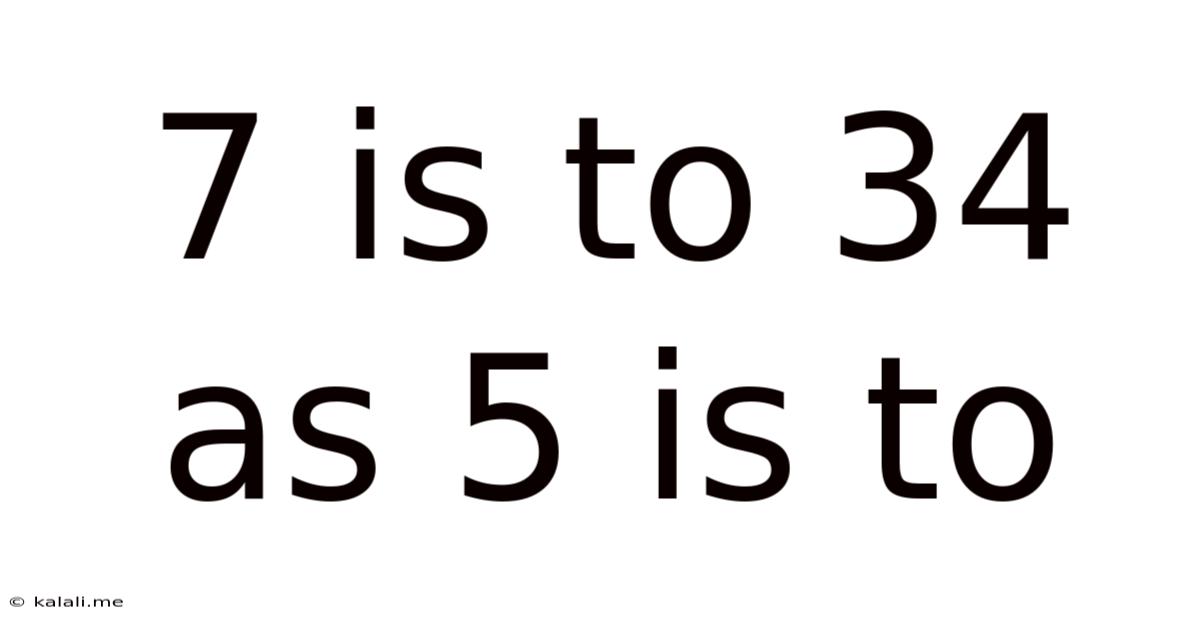
Table of Contents
7 is to 34 as 5 is to: Unraveling the Mathematical Puzzle and Exploring Analogical Reasoning
This seemingly simple mathematical puzzle, "7 is to 34 as 5 is to ?", taps into our ability to recognize patterns and apply analogical reasoning. While a single numerical answer might seem straightforward at first glance, a deeper dive reveals multiple potential solutions depending on the underlying logic applied. This article will explore various approaches to solving this puzzle, highlighting the importance of pattern recognition, logical deduction, and the fascinating world of mathematical relationships. We'll examine different mathematical operations and sequences that could establish a valid analogy, and ultimately show that there isn't just one right answer, but several possibilities depending on the assumed rule.
Meta Description: This article explores the mathematical puzzle "7 is to 34 as 5 is to ?" analyzing multiple potential solutions based on different logical operations and sequences. Discover the diverse approaches to analogical reasoning and the importance of pattern recognition in problem-solving.
Understanding Analogical Reasoning
Before diving into the specifics of the puzzle, it's crucial to understand the concept of analogical reasoning. This type of reasoning involves identifying similarities between two seemingly different things and using those similarities to draw inferences or solve problems. In the context of our puzzle, we are looking for a relationship between 7 and 34 that we can then apply to 5 to find the corresponding number. This requires us to carefully examine the numerical relationship between 7 and 34 and identify the underlying pattern or rule.
Potential Solutions and Their Underlying Logic
Let's explore several possible solutions and the logical reasoning behind them:
1. The "Multiply and Add" Approach:
One possible relationship between 7 and 34 is that 34 is obtained by multiplying 7 by 4 and then adding 10: (7 * 4) + 10 = 34. Following this logic, applying the same rule to 5, we get: (5 * 4) + 10 = 30. Therefore, a possible answer is 30. This approach demonstrates a simple linear relationship with a constant multiplier and additive factor. It showcases a straightforward way to establish an analogy based on a clear mathematical operation.
2. The "Quadratic Relationship":
Another approach involves exploring quadratic relationships. We could observe that 34 is a close approximation of 7 squared (49), reduced by a factor related to 7. It’s a more complex relationship, possibly involving subtracting a multiple of 7 from 7 squared. For example, 49 - 15 = 34. If we apply this approach (x² - (x*k)) where x is the initial number and k is a constant, we need to find a constant 'k' that works for both 7 and 5. This might require some trial and error, and different values of k could lead to different answers. This highlights the importance of considering different mathematical functions and their properties in seeking a valid analogy.
3. The "Sequence-Based" Approach:
Instead of focusing on a single mathematical operation, we can explore whether 7 and 34 are part of a larger sequence. Consider sequences that involve incrementing numbers by a certain pattern. Although this approach is less direct than using arithmetic operations, it demonstrates a wider approach to pattern recognition. We need to identify a sequence where 7 and 34 hold a specific relative position. Determining such a sequence may require more advanced mathematical analysis, including the use of difference tables or other pattern recognition techniques.
4. The "Prime Factorization and Addition" Approach:
This approach involves analyzing the prime factorization of the numbers involved. The prime factorization of 7 is simply 7. The prime factorization of 34 is 2 x 17. We can see that there isn't an immediately apparent relationship between the prime factors themselves, but we can try exploring different combinations and operations. Perhaps adding or subtracting the prime factors could yield a meaningful relationship. This approach requires a deeper mathematical understanding and a more exploratory investigation of number theory principles.
5. The "Geometric Progression (with a Twist)" Approach:
This is a more advanced approach that considers geometric progressions (or geometric sequences), where each number is obtained by multiplying the previous number by a constant. While 7 and 34 are not directly part of a simple geometric progression, we can look for patterns within their multiples or related numbers. A modified geometric progression could be at play, possibly involving an additional additive or subtractive element to maintain a consistent ratio. Exploring this approach may need more iterations and creative mathematical thinking.
6. The "Arbitrary Function Approach":
We could theoretically define an arbitrary function that maps 7 to 34 and then apply the same function to 5. This demonstrates the potential infinity of solutions. While less elegant, it highlights the flexibility of analogical reasoning, demonstrating that we can create rules to justify specific relationships. We can make the argument that an infinite number of functions exist which could link 7 and 34 and consequently, numerous answers are possible depending on which function we choose. This highlights the limitations in assuming that there is only one correct solution for this type of problem.
7. The "Number Theory Approach":
This method focuses on concepts from number theory, like divisors, remainders, congruences, or other number properties. We could explore whether 7 and 34 share any specific divisibility properties or have particular remainders when divided by certain numbers. This opens the door to more sophisticated mathematical analysis, potentially revealing subtle relationships not immediately apparent through basic arithmetic operations.
The Importance of Context and Multiple Solutions
The ambiguity of the puzzle underscores a crucial point: there isn’t always one correct answer when dealing with analogical reasoning, especially in the absence of explicit context. The solution depends entirely on the underlying rule or pattern we choose to establish. This emphasizes the importance of clearly defining the rules and assumptions when solving such puzzles. The multiple solutions presented above demonstrate the rich variety of mathematical relationships and the versatility of analogical reasoning.
Developing Strong Analogical Reasoning Skills
Solving puzzles like "7 is to 34 as 5 is to ?" helps develop crucial cognitive skills:
- Pattern Recognition: Identifying underlying patterns and relationships is fundamental to problem-solving in many areas, not just mathematics.
- Logical Deduction: Drawing conclusions based on evidence and applying rules consistently is a key element of critical thinking.
- Creative Thinking: Exploring different possibilities and developing novel solutions requires creativity and flexibility in thinking.
- Mathematical Fluency: A strong understanding of mathematical concepts and operations makes it easier to manipulate numbers and identify patterns.
By exploring different approaches, we enhance our ability to tackle complex problems requiring analogical reasoning. This type of problem-solving transcends pure mathematics and has applications in various fields such as programming, engineering, scientific research, and even creative arts.
Conclusion: Embracing the Ambiguity and the Power of Pattern Recognition
The puzzle "7 is to 34 as 5 is to ?" presents a delightful challenge that encourages us to think creatively and systematically. The multiple potential solutions, ranging from simple arithmetic operations to more sophisticated mathematical explorations, highlight the power of pattern recognition and analogical reasoning. While there's no single "right" answer, the process of exploring different solutions fosters valuable cognitive skills applicable across diverse disciplines. So, the next time you encounter a seemingly simple mathematical puzzle, remember the diverse possibilities and embrace the richness of mathematical exploration. The journey of discovery is often more rewarding than finding a single definitive answer.
Latest Posts
Latest Posts
-
How Much Is 100 Gallons Of Diesel
Jun 30, 2025
-
How Much Is 50 Gallons Of Water
Jun 30, 2025
-
How Many Laps Around A Football Field Is A Mile
Jun 30, 2025
-
The Ability To Say Clever And Funny Things
Jun 30, 2025
-
How Many Cups Are In A Pound Of Lard
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about 7 Is To 34 As 5 Is To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.