7 Is What Percent Of 8
Kalali
Apr 17, 2025 · 5 min read
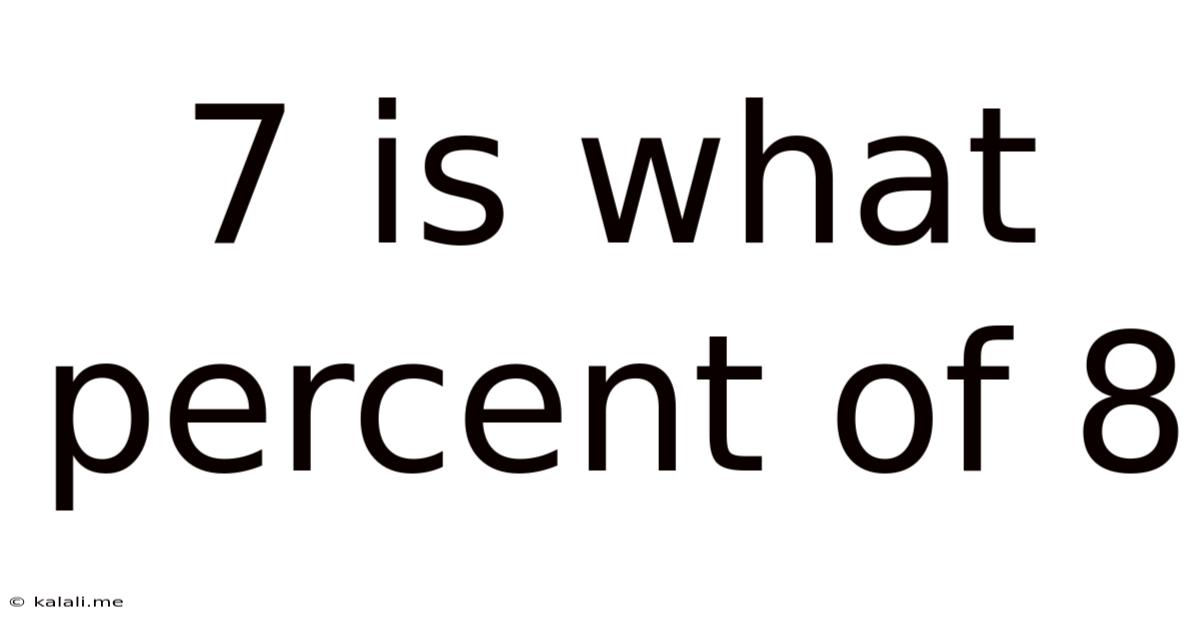
Table of Contents
7 is What Percent of 8? A Deep Dive into Percentage Calculations
This seemingly simple question, "7 is what percent of 8?", opens the door to a fascinating exploration of percentage calculations, their applications in various fields, and the underlying mathematical principles. While the answer itself is straightforward, understanding the why behind the calculation is crucial for mastering this fundamental concept. This article provides a comprehensive guide, explaining not only how to solve this specific problem but also equipping you with the knowledge to tackle any percentage calculation with confidence.
Meta Description: Learn how to calculate percentages with this in-depth guide. We'll solve "7 is what percent of 8?", explain the underlying math, and explore real-world applications of percentage calculations. Master percentages and boost your math skills!
Understanding Percentages: The Foundation
Percentages represent a fraction of 100. The word "percent" literally means "per hundred" (Latin: per centum). Therefore, 1% is equivalent to 1/100, or 0.01. Understanding this basic principle is paramount to understanding percentage calculations. We express percentages using the "%" symbol.
Solving "7 is What Percent of 8?" – The Step-by-Step Approach
To solve this problem, we need to understand that we're looking for a percentage (let's call it 'x%'). This percentage represents the ratio of 7 to 8. We can express this relationship mathematically as:
7 / 8 = x / 100
This equation states that the ratio of 7 to 8 is equal to the ratio of x (our unknown percentage) to 100. To solve for x, we can cross-multiply:
7 * 100 = 8 * x
700 = 8x
Now, we isolate x by dividing both sides of the equation by 8:
x = 700 / 8
x = 87.5
Therefore, 7 is 87.5% of 8.
Alternative Methods for Calculating Percentages
While the above method is a standard approach, several alternative methods can be employed, each offering a slightly different perspective:
-
Using Decimal Conversion: First, divide 7 by 8: 7 ÷ 8 = 0.875. Then, multiply the result by 100 to convert the decimal to a percentage: 0.875 * 100 = 87.5%. This method emphasizes the direct conversion from a ratio to a percentage.
-
Using Proportions: This method, as shown earlier, highlights the proportional relationship between the parts and the whole. It's particularly useful when dealing with more complex percentage problems.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 7 ÷ 8 and then multiply by 100. The calculator will directly provide the answer: 87.5%. This method is efficient but lacks the understanding of the underlying mathematical principles.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life and various professional fields. Here are a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investment all rely heavily on percentage calculations. For example, understanding percentage changes in stock prices is crucial for investors.
-
Retail: Determining discounts (e.g., "20% off"), calculating sales tax, and comparing prices all involve percentages. Consumers use percentage calculations to make informed purchasing decisions.
-
Science: Expressing experimental results, statistical analysis, and data representation often involve percentages. Scientists use percentages to communicate findings clearly and concisely.
-
Education: Grading systems, test scores, and performance evaluations frequently utilize percentages. Students and educators use percentages to track progress and evaluate performance.
-
Healthcare: Calculating dosages of medication, interpreting lab results, and expressing disease prevalence rely on accurate percentage calculations. Medical professionals use percentages for precise and safe medical practices.
Beyond the Basics: More Complex Percentage Problems
While "7 is what percent of 8?" is a relatively simple problem, the principles extend to more complex scenarios. Consider these examples:
-
Finding the Percentage Increase or Decrease: Suppose a price increases from $100 to $120. The percentage increase is calculated as: [(120 - 100) / 100] * 100% = 20%. Similarly, a decrease can be calculated.
-
Calculating Percentages of Percentages: This involves nested percentage calculations. For example, a 10% discount on an item already discounted by 20% requires two sequential percentage calculations.
-
Solving for the Original Value: If you know the percentage and the resulting value, you can work backward to find the original value. For example, if 87.5% of a number is 7, you can solve for the original number (which is 8 in this case).
-
Percentage Points vs. Percentage Change: It’s crucial to understand the difference. A percentage point difference refers to the arithmetic difference between two percentages, while percentage change represents the relative change between two values. For instance, an increase from 10% to 20% is a 10 percentage point increase, but a 100% percentage change.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations.
-
Understand the Underlying Concepts: Don't just memorize formulas; understand the logic behind them.
-
Use Visual Aids: Diagrams and charts can help you visualize the relationships between percentages and quantities.
-
Check Your Answers: Always double-check your calculations to ensure accuracy.
-
Break Down Complex Problems: Divide complex problems into smaller, manageable steps.
Conclusion: The Power of Percentages
The seemingly simple question, "7 is what percent of 8?", unveils a world of mathematical applications and real-world relevance. Mastering percentage calculations is a fundamental skill that transcends academic boundaries and permeates various aspects of life. By understanding the underlying principles and practicing regularly, you can confidently tackle percentage problems of any complexity and unlock their practical applications in your daily life and professional endeavors. Remember the core principle: percentages represent fractions of 100, and mastering this fundamental concept opens doors to a deeper understanding of the world around us. So, the next time you encounter a percentage problem, remember the steps outlined above and approach it with confidence and a clear understanding of the underlying mathematics.
Latest Posts
Latest Posts
-
How Many Cups Are In 20oz
Apr 19, 2025
-
How Many Diagonals Has A Hexagon
Apr 19, 2025
-
9 As A Percentage Of 25
Apr 19, 2025
-
What Is 1 12 In A Decimal
Apr 19, 2025
-
Cuanto Es 39 Fahrenheit En Celsius
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 7 Is What Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.