70 Is What Percent Of 56
Kalali
Apr 24, 2025 · 5 min read
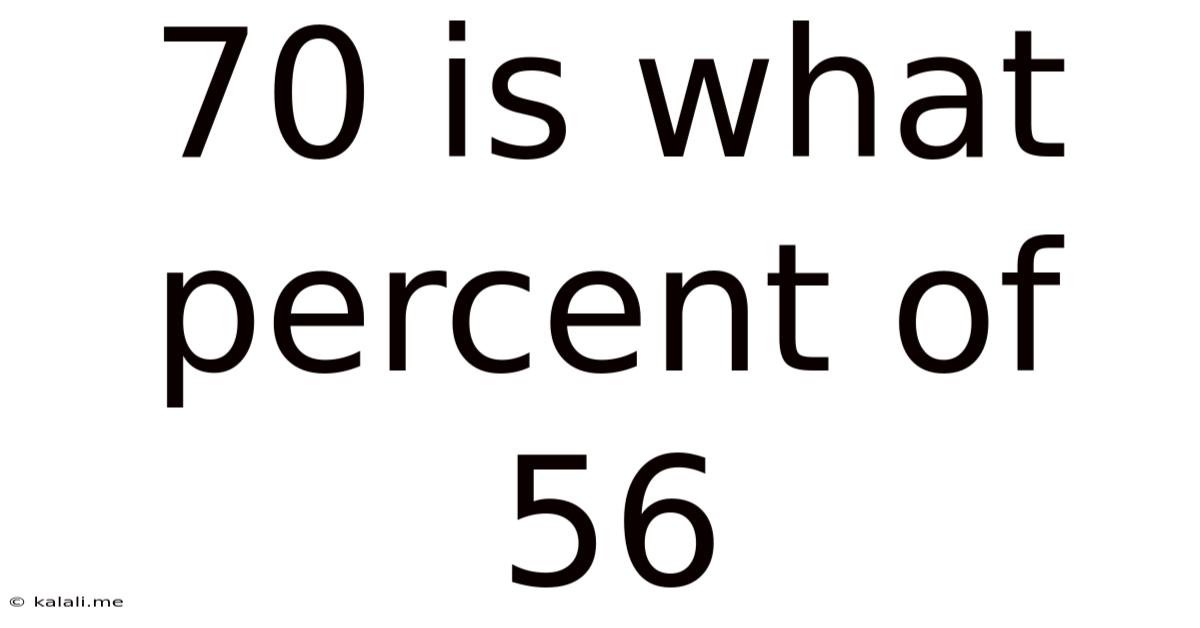
Table of Contents
70 is What Percent of 56? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "70 is what percent of 56?", unlocks a world of practical applications in various fields, from everyday budgeting and shopping to complex scientific analyses and financial modeling. Understanding how to solve this type of problem is crucial for anyone seeking to master fundamental mathematical concepts and apply them to real-world scenarios. This article provides a comprehensive guide, exploring multiple methods to solve this problem and expanding upon the broader concept of percentage calculations. We'll cover everything from the basic formula to advanced techniques, ensuring you gain a thorough understanding and the confidence to tackle similar problems independently.
Understanding Percentages: The Foundation
Before diving into the calculation, let's establish a firm grasp of the core concept: percentages. A percentage represents a fraction of 100. The term "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. This fundamental understanding is key to performing percentage calculations accurately.
Method 1: The Classic Formula Approach
The most straightforward method to determine what percent 70 is of 56 involves utilizing a basic percentage formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 70 (the number we're considering as a portion of the whole)
- Whole: 56 (the total or the base number)
Substituting these values into the formula, we get:
(70 / 56) * 100 = 125%
Therefore, 70 is 125% of 56. This result indicates that 70 exceeds 56 by 25%.
Method 2: Using Proportions
Another effective method involves setting up a proportion. Proportions are mathematical statements that equate two ratios. We can represent our problem as follows:
70/56 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
70 * 100 = 56 * x
7000 = 56x
x = 7000 / 56
x = 125
Again, we arrive at the solution: 70 is 125% of 56. The proportion method offers a clear and organized approach, particularly useful when dealing with more complex percentage problems.
Method 3: Decimal Conversion
This approach utilizes decimal representation to solve the problem. First, we express the relationship between the part and the whole as a decimal:
70 / 56 = 1.25
Then, we convert this decimal to a percentage by multiplying by 100:
1.25 * 100 = 125%
This method provides a concise and efficient way to calculate percentages, particularly suitable when using calculators or spreadsheets.
Interpreting the Result: What Does 125% Mean?
The result of 125% signifies that 70 is larger than 56. The percentage exceeding 100% represents the surplus amount. In this context, 70 is 125% of 56 because it's 25% greater than 56. This interpretation is crucial for comprehending the relative relationship between the two numbers.
Real-World Applications: Percentage Calculations in Daily Life
The ability to calculate percentages isn't just an academic exercise; it's a practical skill applicable in numerous everyday scenarios. Consider these examples:
- Calculating Discounts: Determining the final price of an item after a percentage discount. For example, a 20% discount on a $100 item.
- Calculating Tax: Figuring out the total cost of an item including sales tax.
- Understanding Financial Reports: Analyzing financial statements, interpreting growth rates, and calculating profit margins.
- Assessing Test Scores: Understanding your performance on a test relative to the total possible score.
- Tracking Progress Towards Goals: Monitoring progress towards saving targets, weight loss goals, or fitness milestones.
Advanced Percentage Calculations: Expanding Your Skills
Beyond the fundamental concepts, let's explore some more advanced applications of percentage calculations:
- Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100. For example, if sales increased from $50,000 to $60,000, the percentage increase is [(60,000 - 50,000) / 50,000] * 100 = 20%.
- Calculating Percentage Points: Percentage points represent the arithmetic difference between two percentages. For instance, if interest rates increase from 5% to 8%, the increase is 3 percentage points, not 60%.
- Working with Multiple Percentages: Often, you'll encounter situations involving multiple percentage changes. For example, calculating a discount and then adding sales tax requires performing multiple percentage calculations sequentially.
- Using Percentages in Compound Interest: Understanding how compound interest works involves calculating percentages over time, compounding the interest earned in previous periods.
Troubleshooting Common Mistakes
While percentage calculations are relatively straightforward, several common mistakes can lead to inaccurate results. These include:
- Confusing Percentage Increase with Percentage Points: A common error is misinterpreting percentage points as a percentage increase.
- Incorrect Order of Operations: Failing to follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
- Rounding Errors: Rounding intermediate results can accumulate errors, leading to inaccuracies in the final answer.
Conclusion: Mastering the Art of Percentage Calculations
Understanding how to calculate percentages is a valuable skill with widespread practical applications. Whether it's calculating discounts, analyzing financial data, or simply understanding proportions, the ability to work with percentages empowers you to navigate various real-world scenarios effectively. By mastering the fundamental formulas and techniques discussed in this article, you'll be equipped to tackle percentage-related problems with confidence and accuracy. Remember to practice regularly and explore different approaches to solidify your understanding and build your proficiency in this crucial mathematical concept. The problem "70 is what percent of 56?" serves as an excellent starting point for developing a strong foundation in percentage calculations, enabling you to tackle more complex problems with ease and precision. Remember to always double-check your work and choose the method that feels most comfortable and efficient for you.
Latest Posts
Latest Posts
-
32 Centimeters Equals How Many Inches
Apr 24, 2025
-
How Many Atp Are Created By Fermentation
Apr 24, 2025
-
21 Degrees C Is What In Fahrenheit
Apr 24, 2025
-
20 Cm En Pulgadas Cuanto Es
Apr 24, 2025
-
Cuanto Es 14 Pies En Metros
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about 70 Is What Percent Of 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.