72 Is What Percent Of 80
Kalali
Apr 22, 2025 · 5 min read
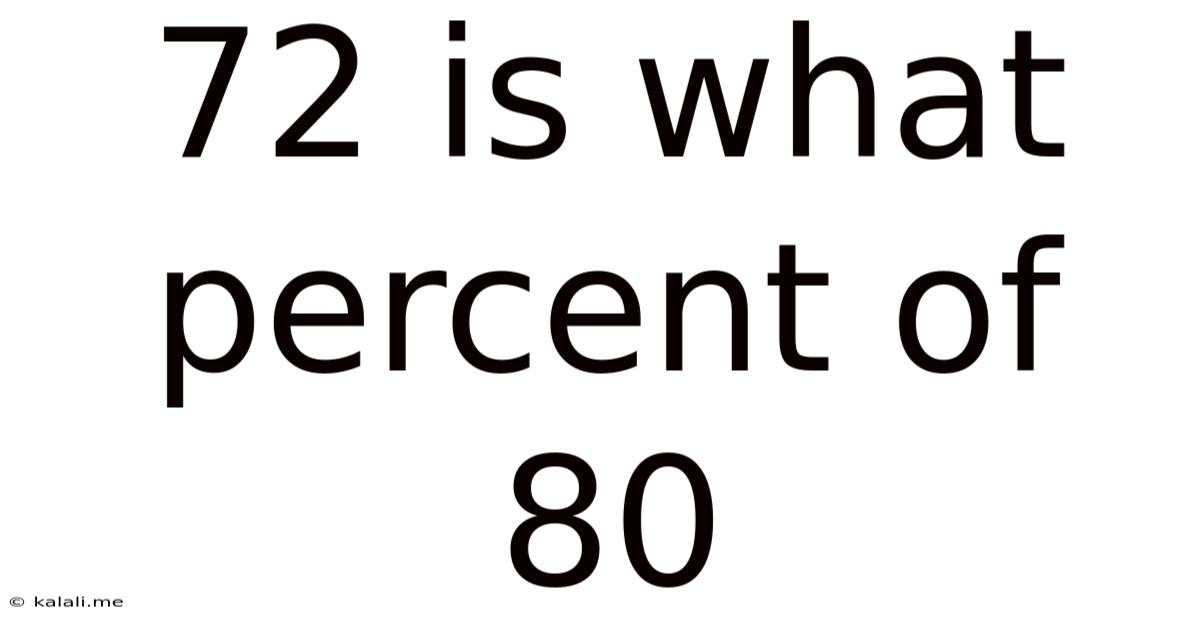
Table of Contents
72 is What Percent of 80? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "72 is what percent of 80?", opens the door to a broader understanding of percentage calculations, a fundamental skill in various aspects of life, from finance and shopping to academic pursuits and data analysis. This article will not only answer the question directly but also delve into the underlying principles, providing you with a comprehensive toolkit for tackling similar problems and a deeper appreciation for the concept of percentages.
Meta Description: Learn how to calculate percentages effectively. This guide provides a step-by-step solution to the problem "72 is what percent of 80?", explores different calculation methods, and offers practical applications of percentage calculations.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2 (one-half). Understanding this basic concept is crucial for mastering percentage calculations.
Method 1: Using the Formula
The most straightforward way to solve "72 is what percent of 80?" is using the fundamental percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 72 (the number we're comparing)
- Whole: 80 (the total number)
Substituting these values into the formula:
(72 / 80) * 100% = 0.9 * 100% = 90%
Therefore, 72 is 90% of 80.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. Proportions are equations that state two ratios are equal. We can represent the problem as:
72/80 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
72 * 100 = 80 * x
7200 = 80x
x = 7200 / 80
x = 90
Therefore, again, 72 is 90% of 80.
Method 3: Using Decimal Equivalents
Percentages can be easily converted to decimals by dividing by 100. Conversely, decimals can be converted to percentages by multiplying by 100. This method offers a different perspective on the problem.
First, find the decimal equivalent of the fraction 72/80:
72 / 80 = 0.9
Next, convert the decimal to a percentage by multiplying by 100%:
0.9 * 100% = 90%
This confirms, once more, that 72 is 90% of 80.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world situations. Here are a few examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $100, you can quickly calculate the discount amount and the final price using percentage calculations. ($100 * 0.20 = $20 discount; $100 - $20 = $80 final price).
-
Understanding Tax Rates: Calculating sales tax or income tax involves percentage calculations. Knowing the tax rate allows you to determine the amount of tax payable on a given amount.
-
Analyzing Financial Statements: Percentage changes in revenue, profit margins, and other financial metrics are crucial for assessing the performance of a business.
-
Calculating Grades: In many academic settings, your final grade is often calculated as a weighted percentage of different assignments and exams.
-
Determining Interest Rates: Understanding compound interest and simple interest requires a firm grasp of percentage calculations. This knowledge is essential for managing personal finances and making informed investment decisions.
-
Interpreting Statistical Data: Percentages are frequently used to represent data in charts, graphs, and reports, facilitating easier interpretation and comparison.
-
Calculating Tips: Determining a suitable tip amount in a restaurant often involves calculating a percentage of the total bill.
-
Understanding Proportions and Ratios: Many real-world problems, from scaling recipes to mixing ingredients, rely on understanding and manipulating ratios and proportions, which are directly related to percentage calculations.
Advanced Percentage Problems
While the example of "72 is what percent of 80?" is relatively straightforward, percentage problems can become more complex. Here are a few variations and how to approach them:
-
Finding the Whole: If you know the part and the percentage, you can calculate the whole. For example, "30 is 60% of what number?" You would rearrange the formula: (Part / Percentage) * 100 = Whole.
-
Finding the Part: If you know the whole and the percentage, you can calculate the part. For example, "What is 40% of 50?" You'd use the standard formula, substituting the known values.
-
Percentage Increase/Decrease: These problems involve calculating the percentage change between two values. The formula is: ((New Value - Old Value) / Old Value) * 100%. For instance, if a stock price rises from $50 to $60, the percentage increase is ((60 - 50) / 50) * 100% = 20%.
-
Compound Percentage Changes: This involves calculating successive percentage changes. For example, if a price increases by 10% and then decreases by 10%, the final price will not be the same as the initial price due to the compounding effect.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering any mathematical skill is consistent practice. Work through various problems to build your confidence and proficiency.
-
Understand the Underlying Concepts: Don't just memorize formulas; understand the logic behind them. This will allow you to adapt your approach to different types of problems.
-
Use a Calculator Strategically: Calculators are valuable tools, but they shouldn't replace your understanding of the underlying concepts. Use them to perform calculations efficiently, but ensure you can perform the calculations manually as well.
-
Break Down Complex Problems: If you encounter a complex percentage problem, break it down into smaller, more manageable steps.
-
Check Your Answers: Always check your answers to ensure accuracy. You can do this by using different methods to solve the same problem or by working backward from your answer.
-
Utilize Online Resources: The internet is a vast resource for learning and practicing percentage calculations. Numerous websites and online tutorials offer explanations, practice problems, and interactive exercises.
Conclusion
The question "72 is what percent of 80?" serves as a springboard for understanding the broader world of percentage calculations. Mastering this fundamental skill empowers you to tackle a wide range of problems across various disciplines, from everyday budgeting to complex financial analysis. By understanding the different calculation methods and practicing regularly, you can develop a strong foundation in percentage calculations and confidently apply this knowledge in your personal and professional life. Remember, consistent practice and a clear understanding of the underlying concepts are the keys to success.
Latest Posts
Latest Posts
-
How Did Dr Kettlewell Test His Hypothesis
Apr 22, 2025
-
109 Cm Is How Many Inches
Apr 22, 2025
-
How Many Grams Is A Half A Pound
Apr 22, 2025
-
How Many Inches Is 7 8
Apr 22, 2025
-
What Is 54 In In Feet
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about 72 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.