75 Is What Percent Of 50
Kalali
Apr 13, 2025 · 5 min read
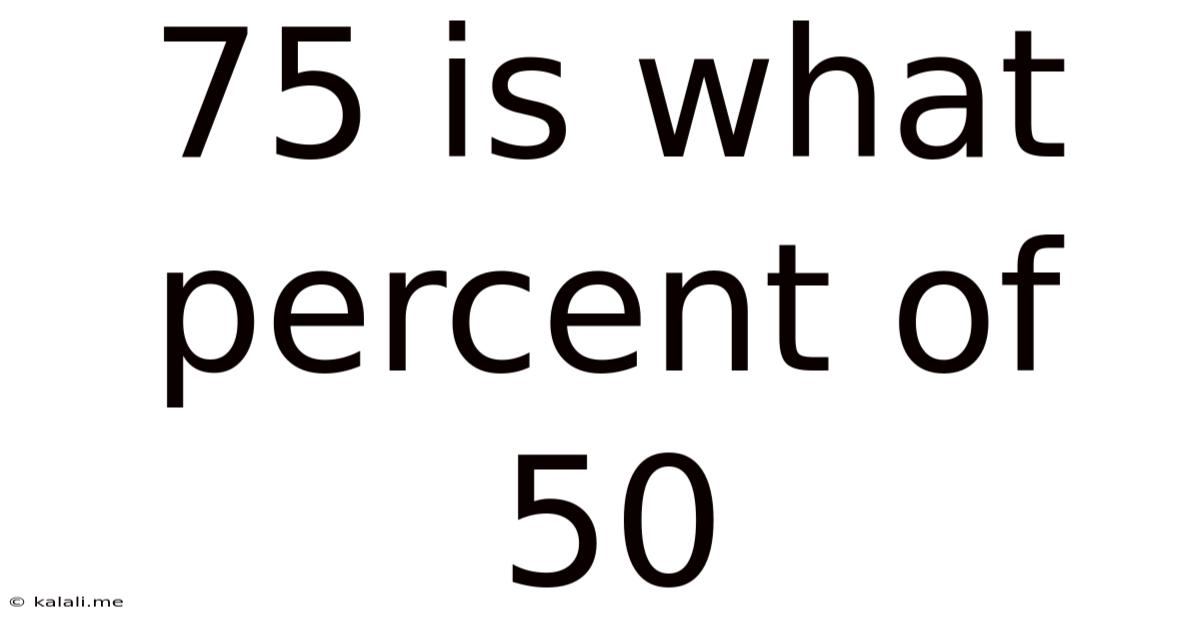
Table of Contents
Decoding Percentages: 75 is What Percent of 50? A Comprehensive Guide
This seemingly simple question, "75 is what percent of 50?", opens the door to a broader understanding of percentages, their applications, and how to solve similar problems with confidence. While the answer might seem counterintuitive at first glance—because 75 is larger than 50—the process of calculating percentages reveals a fundamental concept in mathematics and its real-world applications. This article will not only provide the solution but also delve into the methodology, explore practical examples, and offer strategies for tackling more complex percentage problems.
Meta Description: Learn how to calculate percentages with this in-depth guide. We solve the problem "75 is what percent of 50?" and explore the underlying principles, practical applications, and strategies for mastering percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5. Percentages are used extensively in various fields, including finance, statistics, science, and everyday life, to represent proportions, changes, and comparisons.
Key Concepts:
- Part: The portion of the whole you're interested in. In our example, 75 is the "part."
- Whole: The total amount or the reference value. In our problem, 50 is the "whole."
- Percentage: The ratio of the part to the whole, expressed as a number out of 100. This is what we need to find.
Solving the Problem: 75 is What Percent of 50?
The problem "75 is what percent of 50?" can be solved using a simple formula:
(Part / Whole) * 100% = Percentage
Let's apply this to our problem:
- Part: 75
- Whole: 50
(75 / 50) * 100% = 150%
Therefore, 75 is 150% of 50. This result might initially seem surprising because the "part" (75) is greater than the "whole" (50). This simply indicates that 75 represents 150% of 50 – it's more than the original whole.
Different Approaches to Solving Percentage Problems
While the formula above is straightforward, there are alternative methods to solve percentage problems, each offering a unique perspective:
1. Using Proportions:
This method involves setting up a proportion:
Part/Whole = x/100
Where 'x' represents the percentage we're trying to find. Substituting our values:
75/50 = x/100
Cross-multiplying:
50x = 7500
Solving for x:
x = 7500/50 = 150
Therefore, x = 150%, confirming our previous result.
2. Using Decimal Conversion:
This method converts the percentage to a decimal and then solves the equation. We can rewrite the problem as:
75 = x * 50
To solve for x (which represents the percentage as a decimal):
x = 75 / 50 = 1.5
To convert the decimal back to a percentage, we multiply by 100%:
1.5 * 100% = 150%
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial for navigating various aspects of daily life and professional situations:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentage calculations. For example, understanding compound interest requires a strong grasp of percentage growth.
-
Statistics: Percentages are used to represent data in graphs, charts, and reports. Analyzing survey results, understanding population demographics, and interpreting statistical significance often rely on percentage calculations.
-
Science: Percentages are used to express concentrations of solutions, efficiency of processes, and changes in quantities. For instance, calculating the percentage yield of a chemical reaction is a vital part of experimental work.
-
Retail: Discounts, sales tax, and markups are all expressed as percentages. Consumers need to understand percentage calculations to make informed purchasing decisions.
-
Everyday Life: Calculating tips, understanding nutritional information on food labels, and interpreting statistics in news reports all require familiarity with percentages.
Tackling More Complex Percentage Problems
Once you master the basics, you can tackle more complex percentage scenarios. Here are a few examples:
-
Finding the percentage increase or decrease: This involves calculating the difference between two values and expressing it as a percentage of the original value. For example, if a product's price increased from $50 to $75, the percentage increase is calculated as: [(75-50)/50] * 100% = 50%.
-
Calculating percentages of percentages: This involves applying percentages successively. For example, if you receive a 10% discount on an item already discounted by 20%, the final price is calculated by first applying the 20% discount and then the 10% discount on the resulting price.
-
Solving for the whole when the part and percentage are known: In this case, you know the percentage and the part, and you need to find the whole. For example, if 25% of a number is 50, you can use the formula: (Part / Percentage) * 100 = Whole. This would be (50/25) * 100 = 200. The whole number is 200.
Mastering Percentages: Tips and Tricks
Here are some tips to improve your percentage calculation skills:
-
Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations. Start with simple problems and gradually move to more complex ones.
-
Use different methods: Experiment with various methods (formula, proportions, decimal conversion) to find the approach that best suits your understanding.
-
Check your work: Always verify your answers to ensure accuracy. You can do this by using a different method or estimating the answer before calculating.
-
Utilize online resources: Numerous online calculators and tutorials can provide additional practice and support.
-
Understand the context: Pay close attention to the wording of the problem to avoid misinterpretations.
-
Break down complex problems: Divide complex percentage problems into smaller, manageable steps.
Conclusion
The seemingly straightforward question, "75 is what percent of 50?" serves as a springboard for understanding the fundamental concepts of percentages and their widespread applications. By mastering the methods discussed in this article—including the basic formula, proportions, and decimal conversion—you can confidently tackle various percentage problems encountered in everyday life, academic pursuits, and professional settings. Remember that consistent practice and a clear understanding of the underlying principles are key to mastering percentage calculations. The ability to work with percentages effectively is a valuable skill that enhances problem-solving capabilities and empowers informed decision-making across numerous domains.
Latest Posts
Latest Posts
-
What Is The Surface Area Of The Cube Below
Jul 14, 2025
-
How Many Grams Is Quarter Pound Of Weed
Jul 14, 2025
-
7am To 11pm Is How Many Hours
Jul 14, 2025
-
How Many Squares Of Shingles On A Pallet
Jul 14, 2025
-
What Is The Average Iq For 14 Year Old
Jul 14, 2025
Related Post
Thank you for visiting our website which covers about 75 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.