8 3 As A Mixed Number
Kalali
Apr 04, 2025 · 5 min read
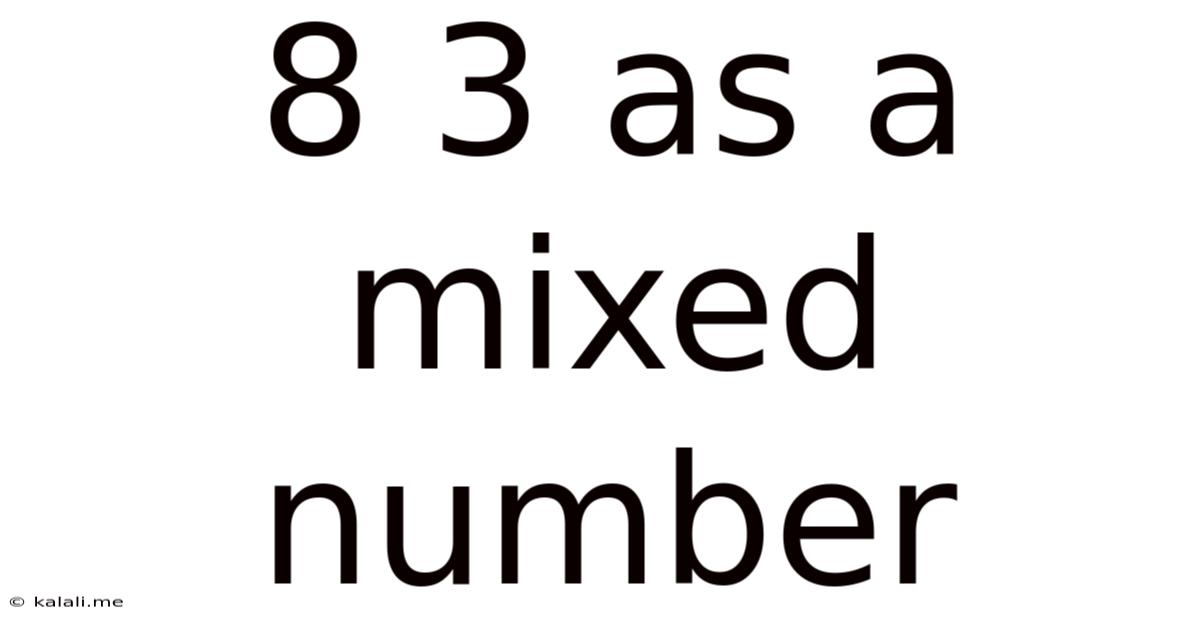
Table of Contents
8/3 as a Mixed Number: A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in everyday life and advanced studies. Converting improper fractions, like 8/3, into mixed numbers is a key aspect of this understanding. This comprehensive guide will delve into the concept of mixed numbers, explore the process of converting 8/3 into a mixed number, and provide practical examples and applications. We'll also look at why understanding this conversion is important and how it applies to various mathematical operations.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For instance, 1/2, 3/4, and 2/5 are all proper fractions. A mixed number represents a quantity that's greater than one. For example, 2 1/2 represents two whole units and one-half of another unit.
Converting an Improper Fraction to a Mixed Number
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 8/3 is an improper fraction because the numerator (8) is larger than the denominator (3). To convert an improper fraction to a mixed number, you need to perform division.
Here's the step-by-step process:
- Divide the numerator by the denominator: Divide 8 by 3.
- Determine the whole number: The quotient (the result of the division) becomes the whole number part of the mixed number. 8 divided by 3 is 2 with a remainder of 2. So, our whole number is 2.
- Determine the fraction: The remainder becomes the numerator of the fraction, and the original denominator remains the same. The remainder is 2, and the denominator is 3. Therefore, the fraction is 2/3.
- Combine the whole number and the fraction: Combine the whole number and the fraction to create the mixed number. This gives us 2 2/3.
Therefore, 8/3 as a mixed number is 2 2/3.
Visual Representation of 8/3
Imagine you have 8 slices of pizza, and each pizza has 3 slices. You can make 2 complete pizzas (that's 2 x 3 = 6 slices) and have 2 slices remaining. This visually represents 2 2/3 pizzas. This visual representation helps to solidify the understanding of the conversion process.
Practical Applications of Converting Fractions to Mixed Numbers
The ability to convert improper fractions to mixed numbers is essential in many real-world situations and mathematical contexts:
- Measurement: Imagine you're measuring ingredients for a recipe. If the recipe calls for 8/3 cups of flour, it's much easier to understand and measure 2 2/3 cups.
- Construction: In construction projects, measurements often involve fractions. Converting improper fractions to mixed numbers allows for easier comprehension and precise calculations.
- Baking: Similar to cooking, baking requires precise measurements. Understanding mixed numbers ensures accurate ingredient proportions.
- Sharing: If you have 8 cookies to share among 3 friends, expressing it as 2 2/3 cookies per friend provides a clearer understanding of the distribution.
- Time: Time is often expressed in mixed numbers (e.g., 1 hour and 30 minutes can be represented as 1 1/2 hours).
- Geometry: Calculating areas and volumes often involves fractions, and converting them to mixed numbers simplifies interpretation.
Why is this Conversion Important?
Converting improper fractions to mixed numbers makes fractions easier to understand and use. Mixed numbers offer a more intuitive representation of quantities larger than one. They are also crucial for performing various mathematical operations such as:
- Addition and Subtraction: Adding and subtracting mixed numbers is generally easier than working solely with improper fractions.
- Multiplication and Division: While multiplying and dividing improper fractions is possible, converting to mixed numbers can sometimes simplify the process. However, converting back to improper fractions is often necessary for these operations to be executed correctly.
- Comparison: Comparing mixed numbers is often more straightforward than comparing improper fractions.
Further Exploration: Working with Mixed Numbers
Beyond the basic conversion, understanding mixed numbers involves several other skills:
- Converting Mixed Numbers to Improper Fractions: This is the reverse process of what we've discussed. To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, converting 2 2/3 back to an improper fraction: (2 x 3) + 2 = 8, so the improper fraction is 8/3.
- Adding and Subtracting Mixed Numbers: When adding or subtracting mixed numbers, it's often easier to convert them into improper fractions first, then perform the operation, and finally convert the result back to a mixed number if needed.
- Multiplying and Dividing Mixed Numbers: Similarly, it's often beneficial to convert mixed numbers into improper fractions before performing multiplication or division.
Troubleshooting Common Mistakes
A common mistake is misinterpreting the remainder. Remember that the remainder becomes the numerator of the fraction in the mixed number. Another common mistake is incorrectly combining the whole number and the fraction. Always ensure the whole number and the fraction are clearly separated to avoid confusion.
Conclusion: Mastering the Mixed Number
Understanding how to convert an improper fraction like 8/3 to a mixed number (2 2/3) is a fundamental skill in mathematics. It's crucial for practical applications across various fields, from everyday tasks to more complex mathematical calculations. By mastering this conversion and understanding the associated concepts, you'll build a stronger foundation in fractions and improve your overall mathematical proficiency. Remember to practice regularly and explore different applications to solidify your understanding. This will greatly enhance your ability to work with fractions and solve real-world problems effectively. The ability to seamlessly transition between improper fractions and mixed numbers will greatly improve your mathematical agility and problem-solving capabilities.
Latest Posts
Latest Posts
-
What Are The Factors Of 38
Apr 10, 2025
-
Cuanto Equivale 100 Pies En Metros
Apr 10, 2025
-
Where In The Atom Are Electrons Located
Apr 10, 2025
-
How Do You Get Rid Of A Square Root
Apr 10, 2025
-
How Many Germ Layers Do Sponges Have
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about 8 3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.