8 5 As A Mixed Number
Kalali
Apr 08, 2025 · 6 min read
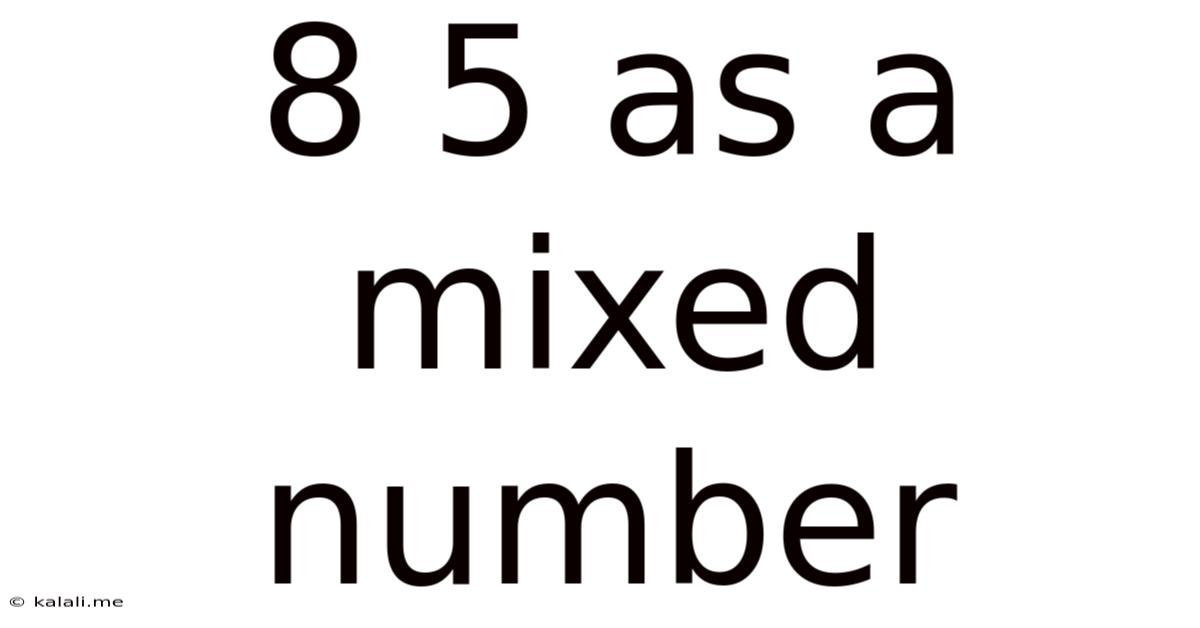
Table of Contents
Understanding 8 5/8 as a Mixed Number: A Comprehensive Guide
Meta Description: This comprehensive guide explores the mixed number 8 5/8, explaining its composition, conversion to improper fractions, practical applications, and related mathematical concepts. Learn how to work with mixed numbers effectively and improve your understanding of fractions.
Mixed numbers, like 8 5/8, are a fundamental concept in mathematics that combines whole numbers and fractions. Understanding them is crucial for various applications, from everyday calculations to advanced mathematical problems. This article provides a detailed exploration of 8 5/8, delving into its properties, conversions, and practical implications. We'll cover everything from the basic definition to advanced applications, making it a valuable resource for students, teachers, and anyone looking to strengthen their understanding of fractions.
What is a Mixed Number?
A mixed number is a number that consists of a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). In the mixed number 8 5/8, '8' represents the whole number, and '5/8' represents the proper fraction. This means we have eight whole units and five-eighths of another unit.
Understanding the Components of 8 5/8
Let's break down the mixed number 8 5/8:
-
8: This is the whole number part. It represents eight complete units. Think of it as having eight full pizzas.
-
5: This is the numerator of the fraction. It represents the number of parts we have. In our pizza analogy, this would be five slices.
-
8: This is the denominator of the fraction. It represents the total number of equal parts a whole is divided into. Sticking with our pizza example, each pizza is cut into eight equal slices.
Converting 8 5/8 to an Improper Fraction
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Converting a mixed number to an improper fraction is a crucial skill. Here's how to convert 8 5/8:
-
Multiply the whole number by the denominator: 8 x 8 = 64
-
Add the numerator: 64 + 5 = 69
-
Keep the same denominator: The denominator remains 8.
Therefore, 8 5/8 is equivalent to the improper fraction 69/8.
Converting an Improper Fraction to a Mixed Number
The reverse process, converting an improper fraction to a mixed number, is equally important. Let's say we have the improper fraction 69/8. Here's how to convert it:
-
Divide the numerator by the denominator: 69 ÷ 8 = 8 with a remainder of 5
-
The quotient becomes the whole number: The quotient 8 becomes the whole number part of the mixed number.
-
The remainder becomes the numerator: The remainder 5 becomes the numerator of the fraction.
-
The denominator remains the same: The denominator remains 8.
Therefore, 69/8 is equivalent to the mixed number 8 5/8.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life and various fields, including:
-
Cooking and Baking: Recipes often call for mixed numbers of ingredients, such as 2 1/2 cups of flour or 1 3/4 teaspoons of baking powder.
-
Measurements: Measuring lengths, weights, and volumes often involves mixed numbers. For example, a piece of wood might be 5 3/4 inches long.
-
Construction and Engineering: Precise measurements are essential in construction and engineering, and mixed numbers are frequently used to represent dimensions and quantities.
-
Data Analysis: Mixed numbers might appear in datasets representing various quantities or measurements.
-
Financial Calculations: Mixed numbers can be used in financial calculations involving shares, portions, and other fractional quantities.
Working with Mixed Numbers: Addition and Subtraction
Adding and subtracting mixed numbers requires careful attention to the fractional parts. Here's a step-by-step guide:
Addition:
Let's add 8 5/8 and 2 3/8:
-
Add the whole numbers: 8 + 2 = 10
-
Add the fractions: 5/8 + 3/8 = 8/8 = 1
-
Combine the results: 10 + 1 = 11
Therefore, 8 5/8 + 2 3/8 = 11
Subtraction:
Let's subtract 3 1/4 from 8 5/8:
-
Find a common denominator: The common denominator for 8 and 4 is 8. Convert 3 1/4 to an improper fraction: (3 x 4 + 1)/4 = 13/4. Then convert 13/4 to an equivalent fraction with a denominator of 8: (13 x 2)/(4 x 2) = 26/8.
-
Convert 8 5/8 to an improper fraction: (8 x 8 + 5)/8 = 69/8
-
Subtract the improper fractions: 69/8 - 26/8 = 43/8
-
Convert the result back to a mixed number: 43 ÷ 8 = 5 with a remainder of 3. Therefore, 43/8 = 5 3/8
Working with Mixed Numbers: Multiplication and Division
Multiplying and dividing mixed numbers involves slightly more complex steps:
Multiplication:
To multiply mixed numbers, it's best to first convert them into improper fractions. Let's multiply 8 5/8 by 2 1/2:
-
Convert to improper fractions: 8 5/8 = 69/8 and 2 1/2 = 5/2
-
Multiply the numerators and denominators: (69 x 5) / (8 x 2) = 345/16
-
Convert back to a mixed number: 345 ÷ 16 = 21 with a remainder of 9. Therefore, 345/16 = 21 9/16
Division:
Similar to multiplication, division of mixed numbers is best performed by converting them to improper fractions. Let's divide 8 5/8 by 2 1/2:
-
Convert to improper fractions: 8 5/8 = 69/8 and 2 1/2 = 5/2
-
Invert the second fraction (reciprocal) and multiply: 69/8 x 2/5 = 138/40
-
Simplify the fraction: 138/40 = 69/20
-
Convert back to a mixed number: 69 ÷ 20 = 3 with a remainder of 9. Therefore, 69/20 = 3 9/20
Simplifying Fractions within Mixed Numbers
Sometimes, the fractional part of a mixed number can be simplified. For example, if we have the mixed number 8 12/16, we can simplify the fraction 12/16 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 4. This simplifies 12/16 to 3/4. Therefore, 8 12/16 simplifies to 8 3/4.
Advanced Applications and Further Exploration
The understanding of mixed numbers extends into more complex mathematical concepts:
-
Algebra: Mixed numbers are used in algebraic equations and expressions.
-
Calculus: While less direct, the foundational understanding of fractions is crucial for calculus.
-
Geometry: Mixed numbers appear in geometric calculations involving lengths, areas, and volumes.
-
Probability and Statistics: Fractional representations, often in mixed number form, are used to represent probabilities and statistical data.
Conclusion
Mastering the concept of mixed numbers, especially understanding a mixed number like 8 5/8, is fundamental to success in mathematics. This article has explored the different aspects of mixed numbers, from their basic definition to their advanced applications. By understanding the conversion between mixed numbers and improper fractions, and by practicing the addition, subtraction, multiplication, and division of mixed numbers, you can build a strong foundation in mathematics and successfully tackle more complex problems. Remember to always simplify your answers where possible to obtain the most efficient and accurate representation of your results. Continual practice and application are key to solidifying your understanding and improving your proficiency with mixed numbers.
Latest Posts
Latest Posts
-
What Is The Lowest Common Multiple Of 3 And 7
Apr 17, 2025
-
2 To The Power Of 40
Apr 17, 2025
-
Cuanto Son 73 Grados Fahrenheit En Centigrados
Apr 17, 2025
-
9 Meters Is How Many Feet
Apr 17, 2025
-
50 Cm Equals How Many M
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 8 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.