8 Is What Percent Of 30
Kalali
Apr 26, 2025 · 5 min read
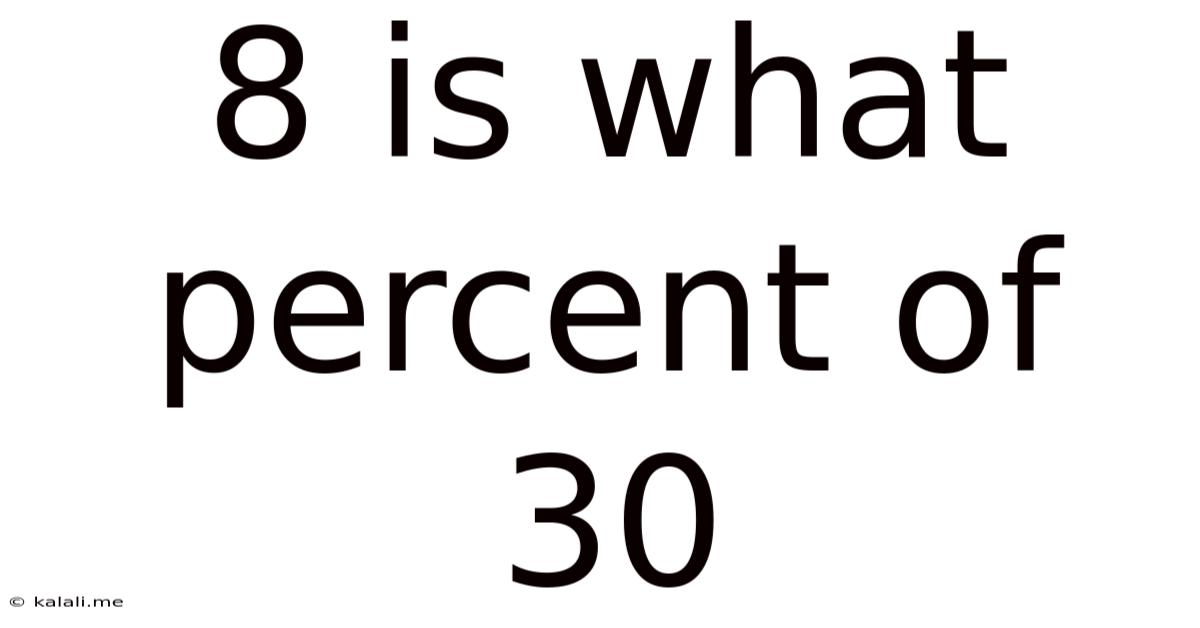
Table of Contents
8 is What Percent of 30? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "8 is what percent of 30?", opens the door to a world of percentage calculations crucial for various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to solve this, and similar problems, is a fundamental skill. This article will provide a comprehensive explanation, covering various methods, practical applications, and related concepts to solidify your understanding of percentages. We'll go beyond just finding the answer and delve into the underlying principles, equipping you with the knowledge to tackle any percentage problem with confidence.
Meta Description: Learn how to calculate percentages effortlessly! This comprehensive guide explains how to determine what percent 8 is of 30, covering multiple methods, practical applications, and related percentage concepts. Master percentage calculations today!
Understanding Percentages: The Basics
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "per hundred." Essentially, a percentage shows the proportional relationship between a part and a whole. For instance, 50% means 50 out of 100, or one-half.
Method 1: Using the Percentage Formula
The most straightforward way to solve "8 is what percent of 30?" is using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 8
- Whole: 30
Substituting these values into the formula:
(8 / 30) * 100% = 26.67% (approximately)
Therefore, 8 is approximately 26.67% of 30. Note that we rounded the answer to two decimal places for practical purposes. Depending on the context, you may need more or fewer decimal places for accuracy.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
8/30 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
30x = 800
x = 800 / 30
x ≈ 26.67%
This method provides an alternative approach to arrive at the same solution. Both methods are equally valid and offer different perspectives on solving percentage problems.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to get the percentage.
First, convert the fraction 8/30 to a decimal by dividing 8 by 30:
8 ÷ 30 ≈ 0.2667
Then, multiply the decimal by 100 to express it as a percentage:
0.2667 * 100% = 26.67%
This approach emphasizes the direct relationship between decimals and percentages, highlighting that a percentage is simply a decimal multiplied by 100.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-life scenarios. Here are a few examples:
-
Calculating discounts: Imagine a shirt priced at $30 is on sale with a 26.67% discount. You can quickly calculate the discount amount ($30 * 0.2667 ≈ $8) and the final price ($30 - $8 = $22).
-
Determining tax amounts: If a state has a 6% sales tax, you can calculate the tax on a $30 purchase ($30 * 0.06 = $1.80) to determine the total cost ($30 + $1.80 = $31.80).
-
Understanding financial statements: Percentage calculations are fundamental in analyzing financial reports, such as calculating profit margins, return on investment (ROI), and growth rates.
-
Analyzing survey data: Percentages are widely used to represent and interpret data from surveys and polls, making it easier to understand trends and patterns.
-
Grade calculations: In education, percentages are used to calculate grades and overall academic performance. For instance, if you scored 8 out of 30 on a quiz, your score would be approximately 26.67%.
-
Calculating tips: Determining an appropriate tip at a restaurant often involves percentage calculations. A 20% tip on a $30 meal would be $6.
Advanced Percentage Concepts and Calculations
Beyond the basic calculation, understanding more advanced concepts is beneficial for tackling complex percentage problems.
-
Finding the whole when the percentage and part are known: This involves rearranging the percentage formula to solve for the whole. For example, if 20% of a number is 6, the number is calculated as (6/0.20) = 30.
-
Calculating percentage change: This involves finding the percentage increase or decrease between two values. The formula is: [(New Value - Old Value) / Old Value] * 100%. For example, an increase from 20 to 30 represents a 50% increase.
-
Compound interest: This involves calculating interest earned not only on the principal amount but also on accumulated interest. This is a crucial concept in finance and investment.
-
Percentage points: It's essential to differentiate between percentage points and percentages. A change from 20% to 30% is a 10 percentage point increase, not a 50% increase.
Common Mistakes to Avoid
-
Confusing percentage and percentage points: As mentioned earlier, remember the difference between these two terms.
-
Incorrect use of the formula: Always ensure you are using the correct formula and substituting the values correctly.
-
Rounding errors: Be mindful of rounding errors, especially when dealing with multiple calculations. Maintain sufficient decimal places throughout your calculations to avoid significant errors in the final result.
-
Not checking your answer: Always verify your answer using a different method or by checking the reasonableness of your result.
Conclusion
Solving "8 is what percent of 30?" may seem simple, but understanding the underlying principles of percentage calculations is crucial for numerous real-world applications. This guide provided various methods to approach this problem, illustrating the flexibility and practicality of percentage calculations. By mastering these techniques and understanding the related concepts, you'll be well-equipped to tackle various percentage problems with confidence and accuracy, whether it involves simple calculations or more complex scenarios in finance, statistics, or other fields. Remember to practice regularly and apply these principles to real-world situations to solidify your understanding and become proficient in percentage calculations.
Latest Posts
Latest Posts
-
100 Kg Is How Many Grams
Apr 26, 2025
-
What Is 22 Centimeters In Inches
Apr 26, 2025
-
How Does Semiconservative Help Prevent Mutations
Apr 26, 2025
-
3 4 Cm Is How Many Inches
Apr 26, 2025
-
What Is 200 Ml In Cups
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.