8 Is What Percent Of 60
Kalali
Apr 27, 2025 · 5 min read
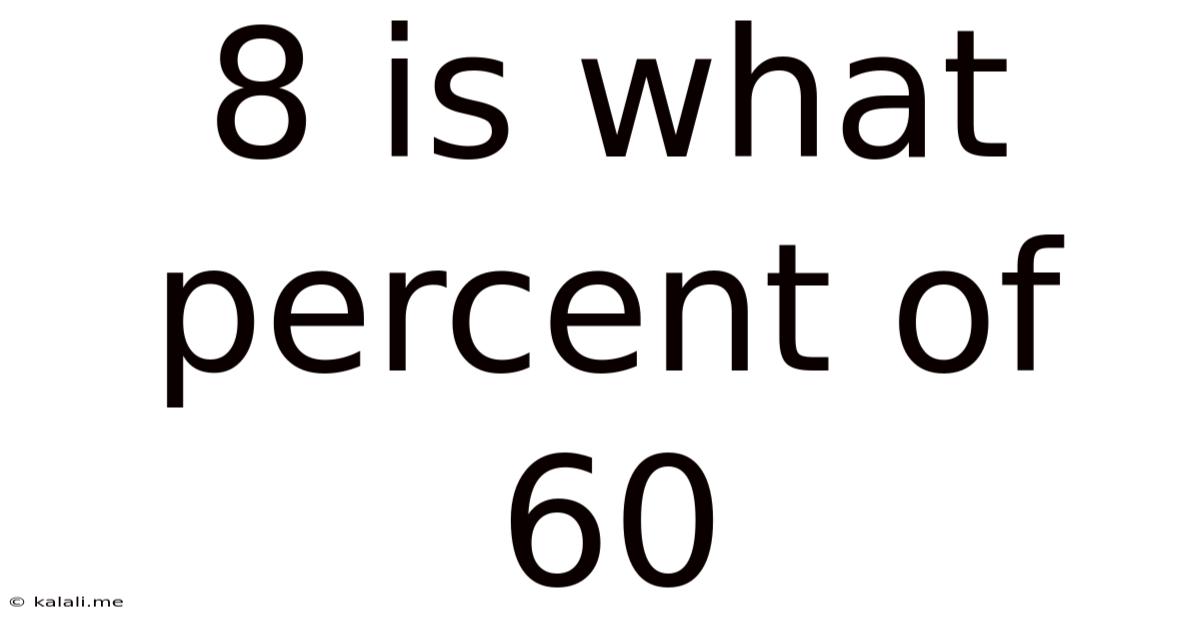
Table of Contents
8 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "8 is what percent of 60?", unlocks a fundamental concept in mathematics with widespread applications in daily life, from calculating discounts and taxes to understanding statistics and financial data. This article will not only answer the question but will provide a thorough exploration of percentage calculations, offering various methods to solve similar problems and illustrating their real-world relevance. We'll delve into the underlying principles, explore different approaches, and equip you with the skills to tackle any percentage problem with confidence. This comprehensive guide covers everything from basic percentage calculations to more advanced applications, making it a valuable resource for students, professionals, and anyone seeking a deeper understanding of percentages.
Understanding Percentages: The Fundamentals
A percentage is simply a fraction expressed as a part of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 1% represents 1/100, or 0.01, of a whole. Understanding this basic definition is crucial for tackling any percentage problem. When you see a percentage, you're essentially looking at a ratio compared to a base of 100.
Method 1: Using the Formula
The most straightforward way to calculate what percent 8 is of 60 is using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 8 (the number we're interested in finding the percentage of)
- Whole: 60 (the total amount)
Substituting these values into the formula:
(8 / 60) x 100 = 13.33%
Therefore, 8 is 13.33% of 60.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion:
8/60 = x/100
Here, 'x' represents the unknown percentage we're trying to find. To solve for 'x', we cross-multiply:
60x = 800
Then, divide both sides by 60:
x = 800 / 60 = 13.33
Therefore, x = 13.33%, confirming the result from the previous method. This method highlights the relational aspect of percentages, showing how a smaller number relates to a larger whole.
Method 3: Using Decimal Conversion
This approach converts the fraction into a decimal and then multiplies by 100 to express it as a percentage.
First, divide the part by the whole:
8 / 60 = 0.1333
Then, multiply the decimal by 100:
0.1333 x 100 = 13.33%
Real-World Applications: Where Percentage Calculations Matter
The ability to calculate percentages is invaluable in many real-world situations. Here are just a few examples:
- Sales and Discounts: Calculating discounts offered during sales is a common application. For example, a 20% discount on a $100 item can be easily calculated using the percentage formula.
- Taxes: Understanding sales tax or income tax involves percentage calculations. Knowing the tax rate allows you to accurately determine the tax amount on a purchase or income.
- Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Calculating the interest earned or owed requires proficiency in percentage calculations.
- Tips and Gratuities: Calculating tips in restaurants or gratuities for services often involves determining a percentage of the total bill.
- Grade Calculations: Students often need to calculate their grades, which are usually expressed as percentages of the total possible points.
- Statistical Analysis: Percentages are fundamental in statistical analysis for representing proportions, frequencies, and changes over time. Data visualization tools often rely on percentage representations for clarity and understanding.
- Financial Reporting: Businesses use percentages extensively in financial statements to represent ratios, profitability, and growth trends. Key performance indicators (KPIs) frequently employ percentages for concise communication.
- Scientific Research: In scientific studies, percentages are essential for reporting experimental results, analyzing data, and drawing conclusions. Results are often represented as a percentage of the total sample size.
Beyond the Basics: More Advanced Percentage Problems
While the "8 is what percent of 60?" question provides a solid foundation, percentage problems can become more complex. Let's explore some variations:
-
Finding the Whole: Instead of finding the percentage, you might be given the percentage and the part, and asked to find the whole. For example: "15% of what number is 6?" This requires rearranging the percentage formula to solve for the whole.
-
Finding the Part: You could be given the percentage and the whole and asked to find the part. For instance: "What is 25% of 80?" This simply involves substituting the known values into the formula.
-
Percentage Increase/Decrease: This involves calculating the percentage change between two numbers. For example: "A product's price increased from $50 to $60. What is the percentage increase?" This requires calculating the difference between the two values, dividing it by the original value, and then multiplying by 100.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It is more complex than simple interest and requires understanding exponential growth principles.
Practical Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice, the more comfortable you will become with percentage calculations. Solve various problems with different scenarios to strengthen your understanding.
- Utilize Online Calculators: While understanding the methods is crucial, online percentage calculators can be helpful for checking your work or quickly solving problems.
- Break Down Complex Problems: If you encounter a complicated percentage problem, break it down into smaller, manageable steps. This approach makes the problem easier to solve.
- Visual Aids: Consider using diagrams or charts to visualize the problem and better understand the relationships between the parts and the whole. This can be particularly helpful for understanding percentage increases and decreases.
- Understand the Context: Always pay close attention to the wording of the problem. Understanding the context helps you choose the correct method and interpret the results correctly.
Conclusion
The question, "8 is what percent of 60?" serves as a gateway to understanding the versatile world of percentage calculations. Mastering this skill empowers you to navigate countless real-world scenarios with confidence. By understanding the fundamental formula, exploring different solution methods, and practicing regularly, you can confidently tackle any percentage problem, transforming seemingly complex calculations into straightforward exercises. The ability to calculate percentages is not merely a mathematical skill; it's a practical tool for success in various aspects of life, from personal finance to professional endeavors. Remember to practice, apply your knowledge to real-world examples, and continue learning to unlock the full potential of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
29 Cm In Inches And Feet
Apr 27, 2025
-
How Much Is 5 Minutes In Seconds
Apr 27, 2025
-
How Much Is 200 Ounces Of Water
Apr 27, 2025
-
What Is Half A Pound In Grams
Apr 27, 2025
-
What Are The Products Of A Reaction
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.