83 Of 200 Is What Percent
Kalali
Apr 15, 2025 · 5 min read
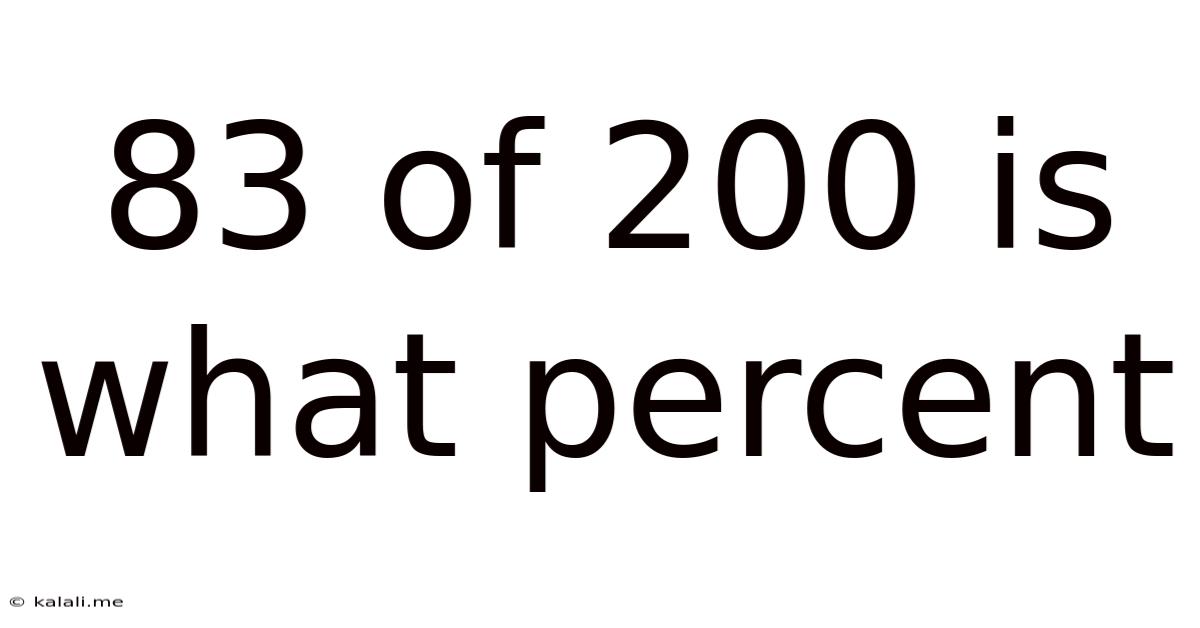
Table of Contents
83 out of 200 is What Percent? A Comprehensive Guide to Percentage Calculations
Determining percentages is a fundamental skill applicable across various fields, from everyday budgeting and shopping to advanced statistical analysis and scientific research. Understanding how to calculate percentages allows you to interpret data, make informed decisions, and communicate numerical information effectively. This comprehensive guide will not only answer the question "83 out of 200 is what percent?" but also equip you with a deeper understanding of percentage calculations and their applications. We will explore various methods, address common misconceptions, and provide practical examples to solidify your understanding.
Meta Description: Learn how to calculate percentages easily! This guide answers "83 out of 200 is what percent?" and provides a comprehensive explanation of percentage calculations, including different methods and real-world applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are a convenient way to represent proportions and compare different quantities.
Method 1: Using Proportions
The most straightforward method to determine what percentage 83 out of 200 represents is to use a proportion. We set up a proportion where x represents the unknown percentage:
83/200 = x/100
To solve for x, we cross-multiply:
200x = 83 * 100 200x = 8300 x = 8300/200 x = 41.5
Therefore, 83 out of 200 is 41.5%.
Method 2: Using Decimal Conversion
Another approach involves converting the fraction 83/200 into a decimal and then multiplying by 100 to express it as a percentage.
First, divide 83 by 200:
83 ÷ 200 = 0.415
Then, multiply the decimal by 100 to convert it to a percentage:
0.415 * 100 = 41.5%
This confirms that 83 out of 200 is indeed 41.5%.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply divide 83 by 200 and then multiply the result by 100. The calculator will directly display the percentage value, which is 41.5%.
Practical Applications of Percentage Calculations
Percentage calculations have wide-ranging applications in various aspects of life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns. For instance, understanding percentage changes in stock prices is crucial for investors. Calculating the percentage increase or decrease in your savings account balance helps you track your financial progress.
-
Science: Expressing experimental results, analyzing data, and representing statistical probabilities. Scientists frequently use percentages to represent the concentration of substances in solutions, the success rate of experiments, or the prevalence of certain characteristics within a population.
-
Retail and Business: Determining discounts, markups, sales tax, and profit margins. Retail businesses heavily rely on percentage calculations for pricing strategies, promotions, and inventory management. Understanding profit margins as a percentage of revenue is critical for evaluating business performance.
-
Education: Calculating grades, assessing test scores, and representing student performance. Teachers utilize percentages to express student grades, track progress, and evaluate overall academic achievement. Understanding your percentage score on an exam provides a clear picture of your performance.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of a sale, and understanding statistics presented in news reports. Daily tasks often involve percentage calculations, such as figuring out the discount on a sale item or calculating the appropriate tip for service.
Understanding Percentage Increase and Decrease
Beyond simply calculating a percentage of a whole, it's crucial to understand how to calculate percentage increases and decreases. These calculations are particularly important when analyzing changes over time or comparing different values.
Percentage Increase: To calculate a percentage increase, you need the original value and the new, increased value. The formula is:
[(New Value - Original Value) / Original Value] * 100%
Percentage Decrease: Similarly, to calculate a percentage decrease, use this formula:
[(Original Value - New Value) / Original Value] * 100%
Example: Let's say the price of a product increased from $100 to $120. The percentage increase would be:
[(120 - 100) / 100] * 100% = 20%
Common Mistakes in Percentage Calculations
Several common mistakes can lead to incorrect results:
-
Confusing the base: Incorrectly identifying the base value (the original amount) in percentage change calculations.
-
Incorrect order of operations: Failing to follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple operations.
-
Rounding errors: Introducing significant errors by rounding intermediate results too early in the calculation. It's often better to carry extra decimal places until the final result.
-
Misinterpreting percentage points: Confusing percentage points with percentage changes. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
Advanced Percentage Calculations: Compound Interest
One significant application of percentages is in the calculation of compound interest. Compound interest is interest earned not only on the principal amount but also on accumulated interest from previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding compound interest is crucial for long-term financial planning, as it significantly impacts investment growth and loan repayments.
Conclusion
This guide has comprehensively explained how to calculate percentages, addressing the specific question "83 out of 200 is what percent?" (41.5%). We've explored various methods, discussed practical applications across diverse fields, highlighted common mistakes to avoid, and touched upon advanced calculations such as compound interest. Mastering percentage calculations is a valuable skill that enhances your analytical abilities and empowers you to make informed decisions in various aspects of your life. Remember to practice regularly and apply these techniques to real-world scenarios to solidify your understanding and improve your proficiency. By understanding the underlying principles and applying the correct methods, you can confidently tackle any percentage-related problem you encounter.
Latest Posts
Latest Posts
-
What Year Would I Be Born If I Was 17
Jul 15, 2025
-
What Is Longer A Kilometer Or A Mile
Jul 15, 2025
-
How Much Does A Full 15 Lb Propane Tank Weigh
Jul 15, 2025
-
Did Chester Wear A Brace On Gunsmoke
Jul 15, 2025
-
How Many Mikes Hard To Get Drunk
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about 83 Of 200 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.