9 Is What Percent Of 10
Kalali
Apr 27, 2025 · 5 min read
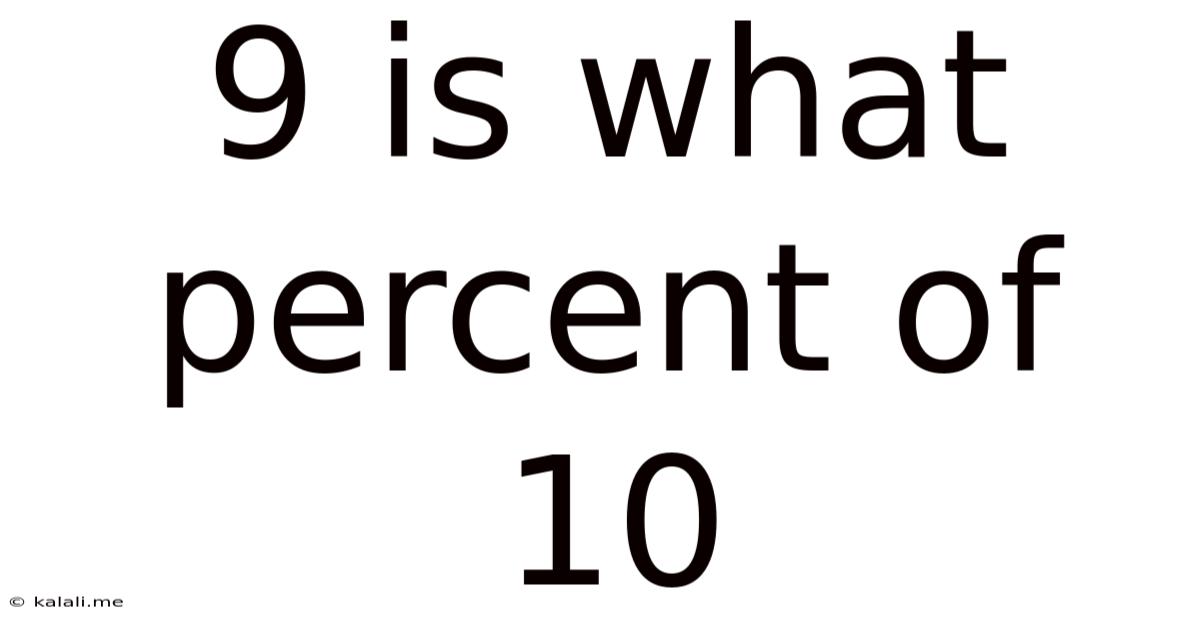
Table of Contents
9 is What Percent of 10? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "9 is what percent of 10?", opens the door to a fascinating exploration of percentages, their calculation, and their widespread applications in various fields. Understanding percentages is fundamental to comprehending many aspects of everyday life, from financial calculations and discounts to scientific data analysis and statistical interpretations. This article will not only answer the initial question but also delve into the underlying concepts, providing you with a comprehensive understanding of percentages and their practical uses.
Meta Description: Discover the answer to "9 is what percent of 10?" and explore the world of percentages. Learn how to calculate percentages, understand their applications, and master this essential mathematical concept. This comprehensive guide covers everything from basic calculations to advanced applications.
Understanding Percentages: A Foundational Concept
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a portion or proportion of a whole, expressed in terms of hundredths. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Understanding this basic definition is crucial for solving percentage problems. It allows us to translate word problems into mathematical equations that can be easily solved.
Calculating Percentages: The Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Where:
- Part: Represents the specific portion you are interested in.
- Whole: Represents the total amount or the entire quantity.
- Percentage: The resulting value expressed as a percentage.
Solving "9 is What Percent of 10?"
Now, let's apply this formula to answer our initial question: "9 is what percent of 10?"
In this case:
- Part = 9
- Whole = 10
Plugging these values into the formula:
(9 / 10) * 100 = 90%
Therefore, 9 is 90% of 10.
Beyond the Basics: Different Types of Percentage Problems
While the basic percentage formula is versatile, many percentage problems require slightly different approaches. Let's explore some common variations:
1. Finding the Percentage Increase or Decrease:
This type of problem involves calculating the percentage change between two values. The formula is:
((New Value - Original Value) / Original Value) * 100 = Percentage Change
For instance, if a product's price increases from $50 to $60, the percentage increase is:
((60 - 50) / 50) * 100 = 20%
2. Finding a Percentage of a Number:
This involves calculating a specific portion of a given number. For example, finding 25% of 80:
(25 / 100) * 80 = 20
3. Finding the Original Value After a Percentage Change:
This problem requires working backward from a percentage change to find the initial value. Let's say a price increased by 15% to reach $76. To find the original price:
Let x be the original price. Then, x + 0.15x = 76. Solving for x gives x = $66.09 (approximately).
Real-World Applications of Percentages
Percentages are ubiquitous in our daily lives, appearing in numerous contexts:
1. Finance and Business:
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding interest rates is crucial for making informed financial decisions.
- Discounts and sales: Retailers use percentages to advertise discounts and sales, making it easy for consumers to understand the price reductions.
- Profit margins: Businesses calculate profit margins as a percentage of their revenue to assess profitability.
- Tax calculations: Taxes are often calculated as a percentage of income or the value of goods and services.
- Investment returns: Investment returns are typically expressed as percentages to show the growth or loss of an investment.
2. Science and Statistics:
- Data representation: Percentages are extensively used in scientific research and statistical analysis to represent proportions and probabilities.
- Error margins: In scientific experiments, error margins are often expressed as percentages to indicate the accuracy of measurements.
- Population statistics: Demographic data, such as population growth rates or unemployment rates, are often expressed as percentages.
3. Everyday Life:
- Tip calculations: Restaurant patrons often calculate tips as a percentage of the total bill.
- Grade calculations: Students' grades are often expressed as percentages to indicate their performance.
- Survey results: Survey results are often presented using percentages to summarize the responses.
- Nutritional information: Food labels indicate the percentage of daily recommended values for various nutrients.
Advanced Percentage Calculations and Concepts
While basic percentage calculations are relatively straightforward, more complex scenarios may require a deeper understanding of mathematical concepts:
1. Compound Interest:
Compound interest involves earning interest on both the principal amount and accumulated interest. This leads to exponential growth, making it a powerful tool for long-term investments but also a significant factor in loan repayments.
2. Percentage Points vs. Percentages:
It's crucial to distinguish between percentage points and percentages. A change of 10 percentage points is different from a 10% increase. For instance, if interest rates increase from 5% to 15%, it is a 10 percentage point increase, but a 200% increase in the interest rate itself.
3. Weighted Averages:
Weighted averages are used when different data points contribute differently to the overall average. This is often seen in calculating GPA, where different courses may carry different credit weights.
Conclusion: Mastering Percentages for Success
Understanding percentages is a fundamental skill with far-reaching applications. From navigating personal finances to analyzing complex data sets, mastering percentage calculations empowers you to make informed decisions and effectively interpret information across diverse fields. This article has provided a comprehensive overview of percentage calculations, diverse applications, and advanced concepts, equipping you to confidently tackle a wide range of percentage-related problems. Remember the basic formula, practice various problem types, and appreciate the pervasive role of percentages in our world. By grasping these concepts, you'll be well-prepared to tackle the numerical challenges that life presents. So, next time you encounter a percentage problem, you'll be equipped to solve it with confidence and accuracy. The simple question "9 is what percent of 10?" serves as a perfect entry point into this vast and important mathematical concept.
Latest Posts
Latest Posts
-
Is A Cell Smaller Than An Atom
Apr 27, 2025
-
What Is 117 Fahrenheit In Celsius
Apr 27, 2025
-
How Many Cm Is 63 In
Apr 27, 2025
-
Cuanto Es 30 Pulgadas En Pies
Apr 27, 2025
-
Cuanto Es 23 Grados Centigrados En Fahrenheit
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 9 Is What Percent Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.