9 Is What Percent Of 16
Kalali
Apr 16, 2025 · 5 min read
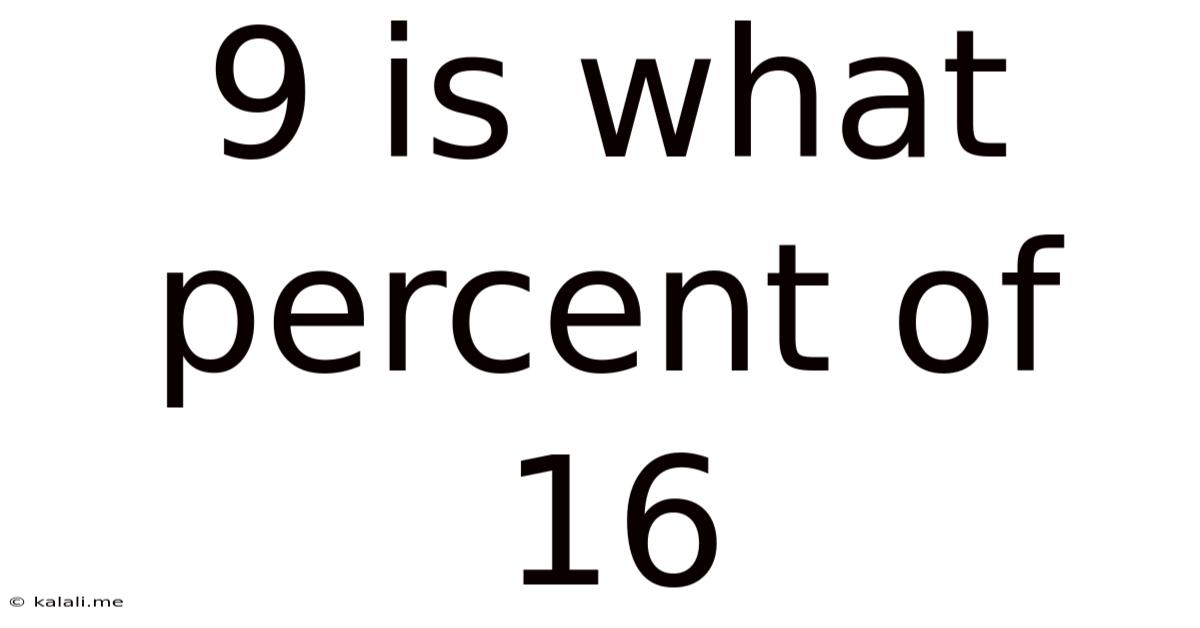
Table of Contents
9 is What Percent of 16? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "9 is what percent of 16?", opens the door to a world of percentage calculations, crucial for numerous applications in everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. This article will not only answer the question directly but also delve into the underlying principles, providing you with a robust understanding of percentage calculations and equipping you with the skills to solve similar problems independently. We'll cover various methods, from basic arithmetic to utilizing calculators and even exploring the concept within the context of proportional reasoning.
Understanding Percentages: The Foundation
Before diving into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is vital for mastering percentage calculations. We often use percentages to represent proportions, ratios, or rates of change. For example, a 10% increase in sales indicates a growth of 10 units for every 100 units previously sold.
Method 1: The Classic Formula
The most straightforward method to determine what percentage 9 is of 16 involves a simple formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 9 (the number we want to express as a percentage)
- Whole: 16 (the total number)
Substituting these values into the formula:
(9 / 16) * 100% = 56.25%
Therefore, 9 is 56.25% of 16.
Method 2: Using Decimal Equivalents
Another approach involves converting the fraction to a decimal first, then multiplying by 100%. This method can be particularly helpful when dealing with more complex fractions.
- Divide the part by the whole: 9 / 16 = 0.5625
- Multiply the decimal by 100%: 0.5625 * 100% = 56.25%
This reinforces the same result: 9 is 56.25% of 16.
Method 3: Proportional Reasoning
This method emphasizes the underlying relationship between the parts and the whole. We can set up a proportion:
9 / 16 = x / 100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
9 * 100 = 16 * x
900 = 16x
x = 900 / 16
x = 56.25
Again, we arrive at the same answer: 9 is 56.25% of 16. This method is particularly useful for understanding the underlying logic and can be easily adapted to various percentage problems.
Method 4: Utilizing a Calculator
For quick calculations, a calculator is invaluable. Most calculators have a percentage function. Simply enter 9 ÷ 16 × 100 =, and the calculator will directly display the result: 56.25%. This method is efficient for time-sensitive situations or when dealing with larger numbers.
Real-World Applications: Putting Percentages to Work
Understanding percentage calculations extends far beyond simple mathematical exercises. Here are some practical examples:
- Sales and Discounts: Imagine a shirt originally priced at $16 is on sale for $9. Using the methods described above, we can easily determine the discount percentage (56.25%).
- Financial Analysis: Percentage calculations are fundamental to analyzing financial statements, calculating profit margins, understanding interest rates, and tracking investment returns. For instance, comparing the percentage growth of a company's revenue year over year provides valuable insights into its financial health.
- Statistics and Data Analysis: Percentages are used extensively in statistical analysis to represent proportions, probabilities, and rates of change within datasets. Understanding these percentages allows for meaningful interpretations of trends and patterns.
- Surveys and Polling: Survey results are often presented in percentages to represent the proportion of respondents who chose specific options. For example, if 9 out of 16 respondents preferred a particular product, the percentage would be 56.25%.
- Grading and Assessment: In many educational systems, grades are often represented as percentages, indicating the proportion of correct answers or the overall performance relative to the total marks available.
Expanding Your Knowledge: Beyond the Basics
While this article focused on a specific problem, the principles extend to more complex scenarios:
- Percentage Increase/Decrease: Calculating the percentage change between two values requires understanding the difference between the new and old values and expressing it as a percentage of the original value. For example, if a value increases from 16 to 25, the percentage increase would be calculated as: ((25-16)/16) * 100% = 56.25%.
- Finding the Whole when the Percentage and Part are Known: This involves a slight alteration of the formula. If you know that 56.25% of a number is 9, you can solve for the whole by reversing the process.
- Compounding Percentages: This involves applying a percentage to a value repeatedly, often used in financial calculations involving interest.
Mastering percentage calculations is a valuable skill that enhances problem-solving capabilities across a wide range of disciplines.
Conclusion: Mastering the Percentage Puzzle
The question, "9 is what percent of 16?" serves as a perfect springboard to explore the world of percentage calculations. We've demonstrated several methods – from the straightforward formula to proportional reasoning and utilizing a calculator – to arrive at the answer: 56.25%. Understanding the underlying principles and practicing with different scenarios will equip you with the confidence to tackle more complex percentage problems in various real-world situations. Remember, percentages are a fundamental tool in interpreting data, making informed decisions, and navigating numerous aspects of daily life. By mastering this concept, you unlock a powerful skill applicable across numerous fields and contexts. So keep practicing, keep exploring, and keep expanding your knowledge of this essential mathematical concept.
Latest Posts
Latest Posts
-
How Many Hours Is 285 Minutes
Apr 19, 2025
-
How Many Species Of Reptiles Are There
Apr 19, 2025
-
6 Cups Equals How Many Pints
Apr 19, 2025
-
How To Do Mole To Mass Conversions
Apr 19, 2025
-
Life Cycle Of A Plant Bean
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 9 Is What Percent Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.