9 Is What Percent Of 3
Kalali
Apr 24, 2025 · 5 min read
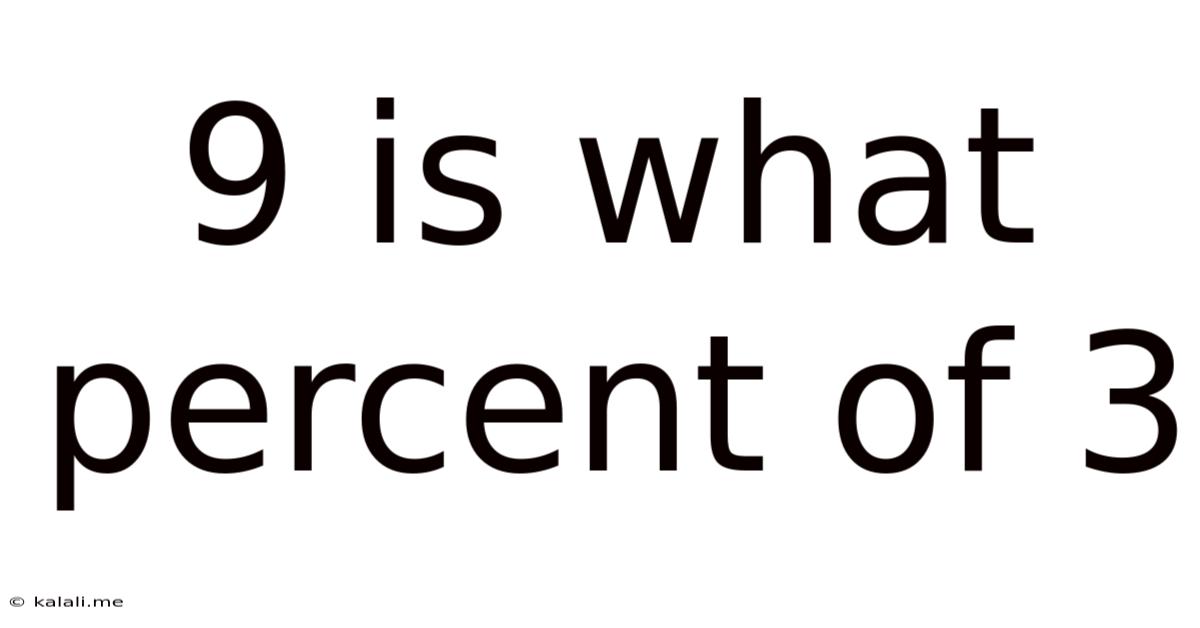
Table of Contents
9 is What Percent of 3? Unpacking the Percentage Calculation and its Applications
This seemingly simple question, "9 is what percent of 3?", opens the door to a deeper understanding of percentages, their applications, and how to solve similar problems with confidence. This article will not only provide the answer but also delve into the underlying mathematical principles, explore various methods of calculation, and showcase real-world examples where understanding percentage calculations is crucial.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "9 is what percent of 3?". This guide covers different calculation methods, real-world applications, and tips for mastering percentage problems.
The immediate answer might seem counter-intuitive. Most people expect a percentage to be less than 100%, yet in this case, the result is far greater. This highlights the importance of understanding the fundamental concept of percentages: they represent a proportion or fraction of a whole, expressed as a number out of 100.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this basic concept is key to solving percentage problems. Think of it this way: a percentage is a standardized way to compare parts of different wholes.
Method 1: Using the Percentage Formula
The most straightforward method to solve "9 is what percent of 3?" involves using the standard percentage formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 9 (the number we want to express as a percentage of the whole)
- Whole: 3 (the total amount)
Substituting these values into the formula:
(9 / 3) * 100 = 300%
Therefore, 9 is 300% of 3.
Method 2: Setting up a Proportion
Another approach is to set up a proportion. A proportion is an equation that states that two ratios are equal. We can represent the problem as:
9/3 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we can cross-multiply:
9 * 100 = 3 * x
900 = 3x
x = 900 / 3
x = 300
Again, this confirms that 9 is 300% of 3.
Method 3: Using Decimal Conversion
We can also solve this using decimal conversion. First, we find the fraction representing the relationship between the parts:
9/3 = 3
Then, we convert this fraction to a percentage by multiplying by 100%:
3 * 100% = 300%
This method provides a concise and efficient way to solve the problem, particularly useful for simple calculations.
Why is the Percentage Greater than 100%?
The result of 300% might seem unusual, but it's perfectly valid. A percentage greater than 100% simply means that the "part" is larger than the "whole." In this instance, 9 is three times larger than 3, hence the 300% result. This often occurs when dealing with growth, increases, or comparisons where the final value exceeds the initial value.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios, including:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all rely heavily on percentage calculations. For instance, determining the interest earned on a savings account or understanding the discount applied during a sale involves precise percentage computations.
-
Business: Businesses use percentages to analyze sales data, track market share, calculate profit margins, and project future growth. Accurate percentage calculations are essential for making informed business decisions. Analyzing the percentage increase or decrease in sales from one period to another, for example, informs strategic planning.
-
Science: Scientists frequently use percentages to express experimental results, such as the percentage of a population exhibiting a specific trait or the percentage change in a measured variable. Percentage errors in measurements are also crucial for assessing experimental accuracy.
-
Everyday Life: Calculating tips at restaurants, determining sale prices in stores, and understanding statistics presented in news reports all involve interpreting and calculating percentages. These day-to-day computations enhance financial literacy and informed decision-making.
Beyond the Basics: More Complex Percentage Problems
While "9 is what percent of 3?" is a relatively straightforward example, the principles extend to more complex problems. For instance:
-
Finding the whole when the part and percentage are known: If 25% of a number is 10, what is the number? This involves reversing the percentage formula.
-
Finding the part when the whole and percentage are known: What is 15% of 80? This requires direct application of the formula.
-
Calculating percentage increase or decrease: If a price increases from $50 to $60, what is the percentage increase? This calculation involves finding the difference, dividing by the original value, and multiplying by 100%.
Mastering these variations necessitates a solid grasp of fundamental percentage concepts and the ability to adapt the standard formula to fit the specifics of each problem. Practice is essential for building fluency and accuracy.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The best way to improve your percentage calculation skills is through consistent practice. Work through various problems, starting with simpler examples and gradually progressing to more complex ones.
-
Understand the Formula: Ensure you fully grasp the basic percentage formula and its variations. Understanding the underlying principles will enable you to approach any percentage problem systematically.
-
Use Different Methods: Experiment with different calculation methods, such as using the formula, setting up a proportion, or employing decimal conversions. Finding the method that best suits your understanding and the complexity of the problem will make calculations more efficient.
-
Check Your Answers: Always double-check your answers to ensure accuracy. You can do this by working through the problem again using a different method or by estimating the answer to see if your result is reasonable.
-
Utilize Online Resources: Many online resources offer interactive exercises and tutorials on percentages. These can be valuable tools for strengthening your understanding and practicing your skills.
Conclusion: The Power of Percentage Understanding
The seemingly simple question, "9 is what percent of 3?" provides a gateway to understanding the pervasive nature of percentage calculations in numerous facets of life. From financial planning to scientific analysis, a firm grasp of percentages is indispensable. By mastering the fundamental formula, practicing regularly, and exploring various solution methods, you can confidently tackle percentage problems and effectively apply this critical skill in diverse contexts. The 300% answer, far from being an anomaly, underscores the versatility and wide-ranging applications of percentage calculations, making it a crucial concept to fully comprehend.
Latest Posts
Latest Posts
-
How Much Is 24 Fluid Ounces
Apr 24, 2025
-
How Much Is 10 Degrees Fahrenheit In Celsius
Apr 24, 2025
-
Which Leukocytes Release Histamine During The Inflammatory Response
Apr 24, 2025
-
What Is 50 Degrees Fahrenheit In Centigrade
Apr 24, 2025
-
8 Cups Is How Many Pints
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about 9 Is What Percent Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.