9 Of 30 Is What Percent
Kalali
Apr 16, 2025 · 5 min read
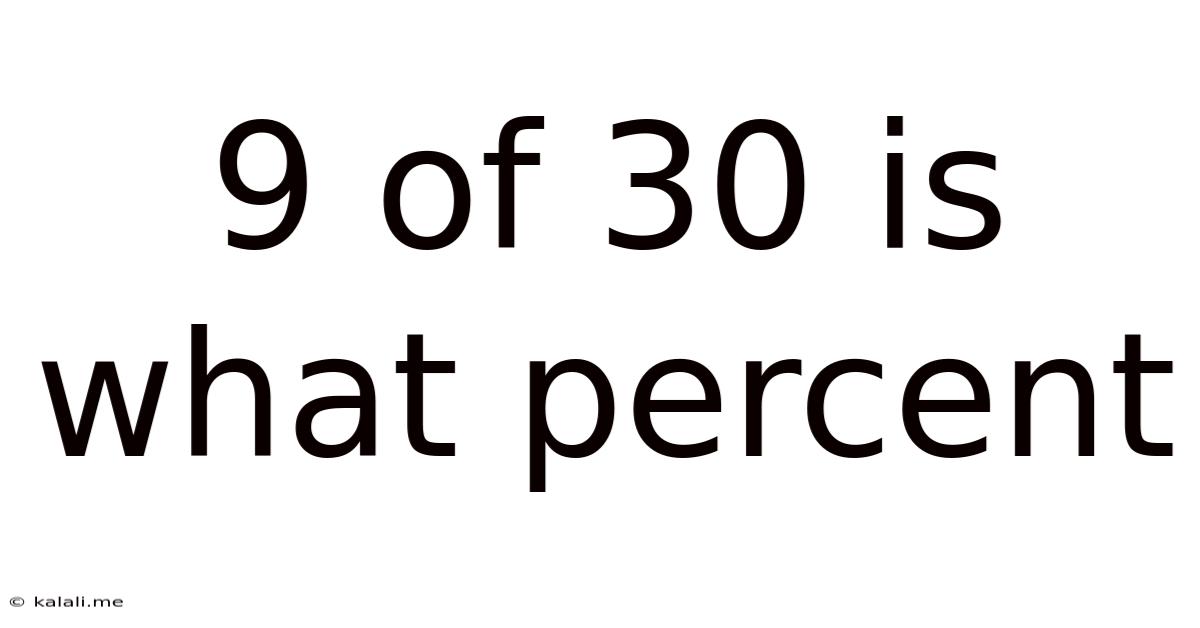
Table of Contents
9 out of 30 is What Percent? A Comprehensive Guide to Percentage Calculations
Meta Description: Learn how to calculate percentages with ease! This in-depth guide explains how to determine what percentage 9 out of 30 represents, covering various methods and practical applications. Master percentage calculations and improve your math skills.
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This comprehensive guide will not only answer the question "9 out of 30 is what percent?" but will also provide you with a thorough understanding of percentage calculations, equipping you with the tools to tackle similar problems confidently.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental concept is crucial to mastering percentage calculations.
Method 1: Using the Formula
The most straightforward method to calculate a percentage is to use the basic percentage formula:
(Part / Whole) * 100% = Percentage
In our case, the "part" is 9, and the "whole" is 30. Let's plug these values into the formula:
(9 / 30) * 100% = 0.3 * 100% = 30%
Therefore, 9 out of 30 is 30%.
Method 2: Simplifying the Fraction
Another approach involves simplifying the fraction before converting it to a percentage. This method can be particularly helpful when dealing with larger numbers.
First, simplify the fraction 9/30:
9/30 can be simplified by dividing both the numerator (9) and the denominator (30) by their greatest common divisor, which is 3:
9 ÷ 3 = 3 30 ÷ 3 = 10
This simplifies the fraction to 3/10. Now, convert this simplified fraction to a percentage:
(3 / 10) * 100% = 30%
Again, we arrive at the answer: 9 out of 30 is 30%.
Method 3: Using a Calculator
Modern calculators are equipped to handle percentage calculations effortlessly. Simply divide the part (9) by the whole (30), and then multiply the result by 100. Most calculators have a percentage button (%) that automates this process.
Practical Applications of Percentage Calculations
Understanding percentages is essential in various real-world scenarios. Here are a few examples:
- Calculating Grades: If you answered 9 questions correctly out of 30 on a test, your score is 30%.
- Discount Calculations: A 30% discount on a $100 item means you save $30 (30% of $100).
- Tax Calculations: A 6% sales tax on a $50 purchase adds $3 in tax (6% of $50).
- Financial Analysis: Analyzing financial statements often involves calculating percentages to understand profit margins, growth rates, and other key indicators.
- Data Analysis: Percentages are widely used in data analysis to represent proportions and trends within datasets. For example, if a survey shows 9 out of 30 people prefer a particular product, that's a 30% preference rate.
- Probability and Statistics: Percentages play a crucial role in expressing probabilities and statistical results.
Expanding Your Percentage Skills: More Complex Examples
Let's explore more complex percentage problems to further solidify your understanding:
Example 1: Finding the Whole
If 30% of a number is 9, what is the number?
We can set up an equation:
0.30 * x = 9
To solve for x, divide both sides by 0.30:
x = 9 / 0.30 = 30
Therefore, the number is 30.
Example 2: Finding the Part
What is 15% of 60?
We use the formula:
(Percentage/100) * Whole = Part
(15/100) * 60 = 9
Therefore, 15% of 60 is 9.
Example 3: Percentage Increase/Decrease
A product's price increased from $30 to $39. What is the percentage increase?
First, find the difference: $39 - $30 = $9
Then, divide the difference by the original price and multiply by 100%:
($9 / $30) * 100% = 30%
The price increased by 30%.
Example 4: Percentage Change from a Different Base
A company's profit increased from $20,000 to $30,000. Calculate the percentage increase.
The increase is $30,000 - $20,000 = $10,000. The percentage increase relative to the original profit is:
($10,000 / $20,000) * 100% = 50%
The profit increased by 50%.
Advanced Percentage Concepts
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest.
- Percentage Points: A percentage point refers to an absolute difference between two percentages. For instance, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
- Weighted Averages: This method accounts for the different weights or importance of different data points when calculating an average percentage.
Troubleshooting Common Percentage Calculation Mistakes
- Incorrect Formula Application: Double-check that you're using the correct formula and plugging in the values accurately.
- Decimal Errors: Be mindful of decimal points when performing calculations. A misplaced decimal can significantly alter the result.
- Unit Confusion: Always ensure you're working with consistent units.
- Misunderstanding Percentage Points: Remember the difference between a percentage change and percentage points.
Conclusion
Calculating percentages is a valuable skill with widespread applications. By mastering the basic formula and practicing different problem types, you can confidently tackle a wide range of percentage-related challenges. This guide has provided various methods to solve the problem "9 out of 30 is what percent?", along with practical examples and explanations to enhance your understanding of percentage calculations. Remember to practice regularly to solidify your skills and build confidence in your mathematical abilities. With consistent effort, you'll become proficient in handling percentages in various contexts.
Latest Posts
Latest Posts
-
How Many 32 Oz Make A Gallon
Jul 12, 2025
-
700 Is 10 Times As Much As
Jul 12, 2025
-
How Much Is 120 Kilograms In Pounds
Jul 12, 2025
-
Born In 1990 How Old Am I
Jul 12, 2025
-
What Is The Average Iq For A 5 Year Old
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about 9 Of 30 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.