90 Out Of 125 As A Percentage
Kalali
Apr 01, 2025 · 5 min read
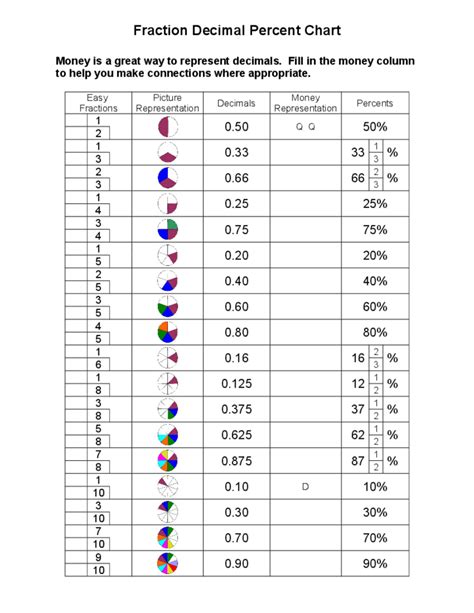
Table of Contents
90 out of 125 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various fields, from everyday finances to complex statistical analyses. Understanding how to convert fractions into percentages is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will delve into the specifics of calculating "90 out of 125 as a percentage," providing a detailed explanation of the process and exploring related percentage calculation techniques. We'll also look at real-world applications and how to confidently approach similar problems in the future.
Understanding Percentages
A percentage represents a fraction of 100. It expresses a proportion relative to a whole. The symbol "%" signifies percentage. For example, 50% means 50 out of 100, which is equivalent to one-half (½) or 0.5 as a decimal.
Calculating 90 out of 125 as a Percentage
The core method involves converting the given fraction (90/125) into a percentage. This can be achieved through two primary approaches:
Method 1: Using the Fraction Method
-
Form the Fraction: Represent the given information as a fraction: 90/125. This signifies 90 parts out of a total of 125 parts.
-
Convert to a Decimal: Divide the numerator (90) by the denominator (125): 90 ÷ 125 = 0.72
-
Convert to a Percentage: Multiply the decimal result by 100: 0.72 x 100 = 72%
Therefore, 90 out of 125 is 72%.
Method 2: Using Proportions
This method uses the concept of proportions to solve for the unknown percentage.
-
Set up a Proportion: We can set up a proportion as follows:
90/125 = x/100Where 'x' represents the percentage we want to find.
-
Cross-Multiply: Cross-multiply to solve for x:
90 * 100 = 125 * x9000 = 125x -
Solve for x: Divide both sides by 125:
x = 9000 ÷ 125 = 72
Therefore, x = 72%, confirming that 90 out of 125 is 72%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous everyday situations:
Finance and Budgeting
- Interest Rates: Calculating interest earned on savings accounts or interest paid on loans involves percentages.
- Discounts and Sales: Determining the final price after a percentage discount requires understanding percentage calculations.
- Taxes: Calculating sales tax, income tax, or other taxes often involves percentage computations.
- Investment Returns: Analyzing investment performance and calculating returns often uses percentages.
- Budget Allocation: Distributing a budget across different categories frequently requires percentage allocation.
Statistics and Data Analysis
- Data Representation: Percentages are crucial for representing data in charts, graphs, and tables, making information easily understandable.
- Probability and Statistics: Calculating probabilities and analyzing statistical data often necessitates percentage calculations.
- Surveys and Polls: Results from surveys and polls are frequently expressed in percentages.
- Data Interpretation: Understanding percentage changes helps in interpreting trends and patterns within data sets.
Science and Engineering
- Concentration and Mixtures: Determining the concentration of solutions or mixtures often involves percentage calculations.
- Efficiency and Productivity: Measuring efficiency and productivity in various processes often utilizes percentages.
- Error Analysis: Expressing errors or uncertainties in measurements frequently involves percentages.
Everyday Life
- Tips and Gratuities: Calculating tips at restaurants or service businesses relies on percentage calculations.
- Comparing Prices: Comparing prices of items with different sizes or quantities often involves percentage calculations to determine the best value.
- Grading and Scores: Understanding percentages is crucial for interpreting scores in exams, tests, or other assessment methods.
Advanced Percentage Calculations: Beyond the Basics
While calculating 90 out of 125 is straightforward, let's explore some more complex percentage-related scenarios:
Finding the Original Value
Suppose you know that 72% of a number is 90. How do you find the original number?
-
Set up an Equation: Let 'x' be the original number. We can write the equation:
0.72x = 90 -
Solve for x: Divide both sides by 0.72:
x = 90 ÷ 0.72 = 125
Therefore, the original number is 125.
Calculating Percentage Increase or Decrease
Suppose a value increases from 90 to 125. What is the percentage increase?
-
Find the Difference: Calculate the difference between the new and old values: 125 - 90 = 35
-
Calculate the Percentage Increase: Divide the difference by the original value and multiply by 100:
(35 ÷ 90) x 100 ≈ 38.89%
Therefore, there is approximately a 38.89% increase.
Similarly, if a value decreases, you can calculate the percentage decrease using the same principle, but using the decrease in value instead of the increase.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice percentage calculations, the more comfortable and confident you'll become.
- Understand the Concepts: A strong grasp of the underlying concepts—fractions, decimals, and proportions—is crucial for accurate calculations.
- Use a Calculator: For complex calculations or large numbers, using a calculator can save time and improve accuracy.
- Check Your Work: Always double-check your calculations to avoid errors.
- Break Down Complex Problems: Divide complex problems into smaller, manageable steps.
- Utilize Online Resources: Numerous online resources, including calculators and tutorials, can help you improve your percentage calculation skills.
Conclusion
Calculating percentages is a versatile and essential skill applicable in various facets of life. This guide has detailed the process of determining "90 out of 125 as a percentage," emphasizing both the fundamental approach and more advanced techniques. By understanding the principles involved and practicing regularly, you can confidently tackle percentage calculations in diverse contexts, making informed decisions and enhancing your analytical abilities. Remember that consistent practice is key to mastering this fundamental mathematical skill, allowing you to navigate numerical challenges effectively and confidently in all your endeavors.
Latest Posts
Latest Posts
-
How To Find Mean In Stem And Leaf Plot
Apr 02, 2025
-
What Is The Lowest Common Multiple Of 4 And 9
Apr 02, 2025
-
What Is The Equation For Photosynthesis And Cellular Respiration
Apr 02, 2025
-
What Is The Third Planet From The Sun
Apr 02, 2025
-
105 Out Of 120 As A Percentage
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 90 Out Of 125 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
