A Cube Plus B Cube Plus C Cube Ka Sutra
Kalali
Jun 15, 2025 · 3 min read
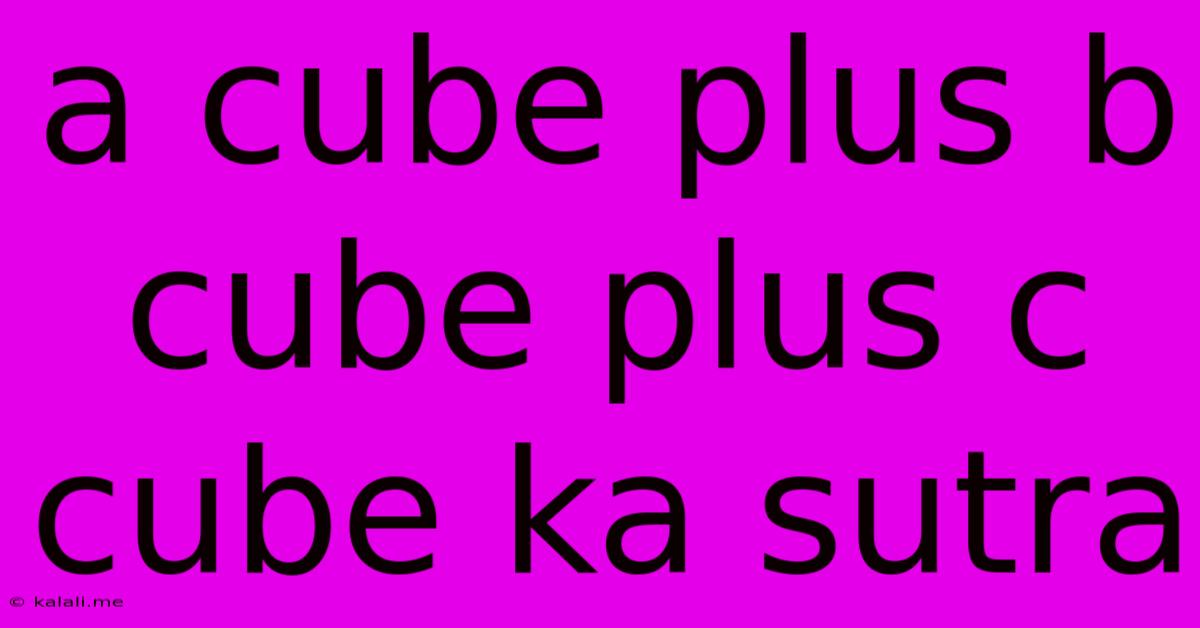
Table of Contents
A Cube Plus B Cube Plus C Cube Ka Sutra: Unraveling the Mathematical Formula
This article delves into the intriguing mathematical formula often referred to as "a cube plus b cube plus c cube ka sutra" – the formula for the sum of cubes. While there isn't a single, universally accepted "sutra" (formula) for the sum of three cubes, we can explore the algebraic expressions and techniques used to solve problems involving a³ + b³ + c³ . This exploration will cover the fundamental concepts, provide examples, and discuss the limitations of finding a direct, concise formula. Understanding this topic will enhance your problem-solving skills in algebra and beyond.
Understanding the Challenge: Why No Simple Formula?
Unlike the sum of squares (a² + b²) or the sum of cubes for two variables (a³ + b³), a straightforward, readily applicable formula for a³ + b³ + c³ doesn't exist. The reason lies in the complexities introduced by adding a third variable. While we can manipulate the expression algebraically, the resulting equations are often lengthy and not easily memorized as a single "sutra."
Exploring Algebraic Manipulations
We can approach the problem using various algebraic techniques. One common approach involves factoring, but this frequently leads to conditional results depending on the relationship between a, b, and c. For example, if a + b + c = 0, we can utilize the identity:
a³ + b³ + c³ - 3abc = (a + b + c)(a² + b² + c² - ab - bc - ca)
If a + b + c = 0, then the entire expression simplifies to a³ + b³ + c³ = 3abc. This provides a neat solution in specific cases, highlighting the conditional nature of any "formula" for a³ + b³ + c³.
Examples and Applications
Let's consider a few examples to illustrate the application of the above identity and the importance of understanding the relationship between a, b, and c:
Example 1: If a = 2, b = -1, and c = -1, then a + b + c = 0. Applying the identity:
2³ + (-1)³ + (-1)³ = 3(2)(-1)(-1) = 6
This shows the simplification possible when a + b + c = 0.
Example 2: If a = 1, b = 2, and c = 3, then a + b + c ≠ 0. In this case, we cannot directly use the simplified formula. We need to calculate the sum directly:
1³ + 2³ + 3³ = 1 + 8 + 27 = 36
This illustrates the need for a different approach when the condition a + b + c = 0 isn't met.
Beyond the Simple Cases
For situations where a + b + c ≠ 0, the problem becomes more involved. There isn't a concise formula comparable to the sum of two cubes. Instead, we'd resort to direct computation or more sophisticated algebraic techniques, which can become complex depending on the values of a, b, and c.
Conclusion: Understanding the Nuances
The search for a single, universal "a cube plus b cube plus c cube ka sutra" is, therefore, a quest for a simplification that doesn't always exist. While the identity for the case where a + b + c = 0 provides a shortcut, a broader understanding of algebraic manipulation is crucial for handling various scenarios. Mastering these techniques allows you to tackle problems involving the sum of three cubes effectively, even without a simple, memorizable formula. Remember, mathematical problem-solving often involves strategic application of various methods rather than a reliance on a single "sutra" for every situation.
Latest Posts
Latest Posts
-
The First Step In The Research Process Is To
Jun 15, 2025
-
Suez Canal Connects Which Two Bodies Of Water
Jun 15, 2025
-
Ammeter Is Connected In Series Or Parallel
Jun 15, 2025
-
What Is A Antonym For Abundant
Jun 15, 2025
-
Triangles Abc And Def Are Similar
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about A Cube Plus B Cube Plus C Cube Ka Sutra . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.