A Hexagon With Exactly 1 Pair Of Parallel Sides
Kalali
Jun 30, 2025 · 5 min read
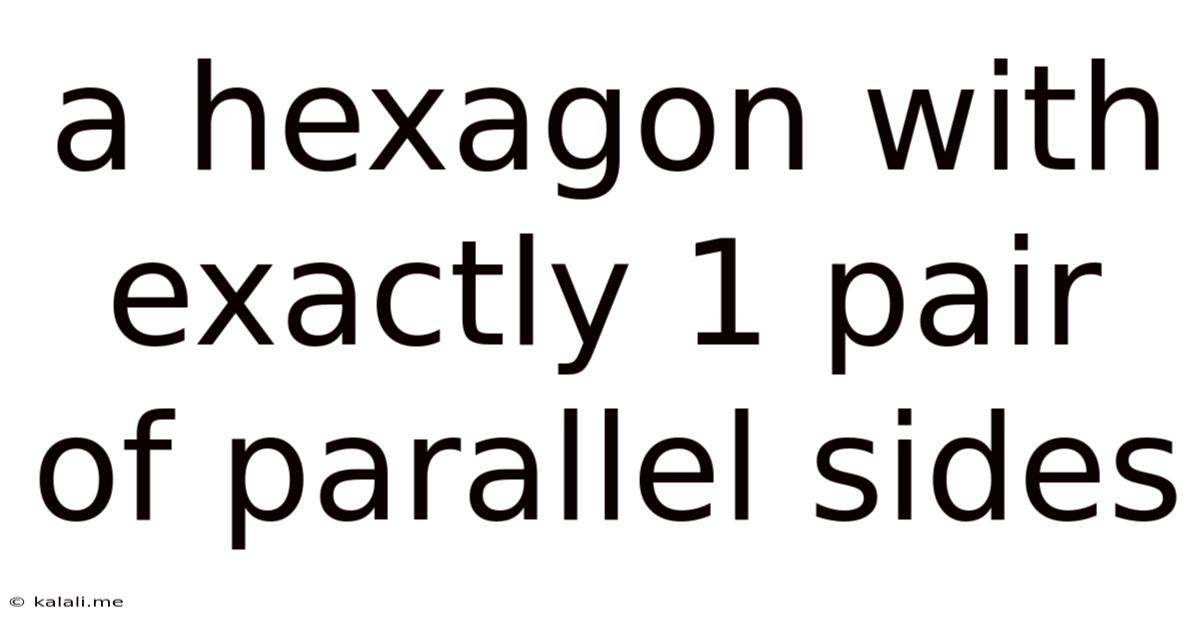
Table of Contents
A Hexagon with Exactly One Pair of Parallel Sides: Exploring its Unique Properties
This article delves into the fascinating geometric properties of a hexagon possessing only one pair of parallel sides. While regular hexagons, with their six equal sides and angles, are commonly understood, this specific type of hexagon presents a richer, more complex geometric puzzle. We will explore its classification, potential construction methods, area calculations, and the implications of its unique parallel sides. Understanding this shape requires a blend of geometric intuition and rigorous mathematical analysis.
What Defines This Hexagon?
A hexagon, by definition, is a six-sided polygon. The crucial characteristic distinguishing this particular hexagon is the presence of exactly one pair of parallel sides. This immediately sets it apart from other hexagons, including parallelograms (with two pairs of parallel sides), trapezoids (with at least one pair of parallel sides), and irregular hexagons with no parallel sides. This single constraint opens up a realm of geometric possibilities, demanding a closer investigation into its properties. We can classify this hexagon as a trapezoidal hexagon, given its inclusion of at least one pair of parallel sides.
Constructing the Hexagon: A Practical Approach
Constructing a hexagon with exactly one pair of parallel sides requires a strategic approach. Several methods exist, each offering a unique perspective on the shape's underlying geometry. One approach involves starting with the parallel sides, establishing their length and distance apart. From the endpoints of one parallel side, you can then draw two lines of arbitrary length and angle, forming two more sides of the hexagon. The final two sides would then need to be drawn to connect the remaining vertices, ensuring that no additional pairs of parallel sides are created. This method emphasizes the freedom in choosing the lengths and angles of non-parallel sides, highlighting the variability of this hexagon type. Alternatively, one could begin by constructing a trapezoid, which inherently has one set of parallel sides. Adding two additional sides to complete the hexagon while maintaining only the single parallel pair presents a more challenging yet potentially more precise construction process.
Exploring the Internal Angles: Summation and Relationships
The sum of the interior angles of any hexagon is always 720 degrees. However, the distribution of these angles within our hexagon with exactly one pair of parallel sides is far from uniform. The angles adjacent to the parallel sides will have specific relationships. If we label the parallel sides as AB and CD, angles A and B will be supplementary to angles C and D respectively. That is, A + C = 180 degrees and B + D = 180 degrees. However, angles E and F remain largely independent, constrained only by the overall sum of interior angles. This uneven distribution of angles is a defining characteristic, highlighting the asymmetrical nature of this specific hexagonal shape.
Calculating the Area: A Multifaceted Problem
Determining the area of this hexagon presents a more complex challenge than simpler polygons. Standard area formulas for regular hexagons or even trapezoids are inapplicable. The most straightforward approach involves breaking down the hexagon into smaller, more manageable shapes. This could involve dividing the hexagon into triangles and trapezoids, calculating the areas of these individual components using standard geometric formulas, and then summing them to find the total area. The accuracy of this method relies heavily on precise measurements of the sides and angles. Alternatively, using coordinate geometry offers a more sophisticated solution. By assigning coordinates to each vertex and using integration techniques, one can accurately calculate the area of the hexagon. However, this method necessitates a more advanced mathematical understanding. The choice of approach depends largely on the available information and the desired level of precision.
Variations and Special Cases:
The "hexagon with exactly one pair of parallel sides" category encompasses a broad range of shapes. There are numerous variations based on the relative lengths of the sides and the magnitudes of the internal angles. A special case arises when the non-parallel sides exhibit specific relationships, leading to certain symmetries or special geometric properties. For instance, if the non-parallel sides are of equal length and angles have particular relationships, we might find some unexpected geometrical properties. These variations add to the richness of the study and require careful consideration in any analysis.
Applications and Relevance: Beyond Pure Geometry
While seemingly abstract, the study of this unique hexagon type is not merely an academic exercise. Understanding its properties can have applications in various fields. In architecture and engineering, this hexagon might find relevance in designing structures with specific load-bearing requirements. The ability to manipulate its shape and calculate its area precisely is crucial for structural stability and load distribution. Moreover, in computer graphics and game development, accurate representation and manipulation of such irregular shapes are crucial for realistic simulations and modeling of complex environments. Even in tiling and pattern design, understanding the properties of this hexagon could unlock unique aesthetic possibilities.
Advanced Considerations: Isoperimetric Inequalities and Optimization Problems
The study can be extended further into advanced areas of mathematics. Isoperimetric inequalities, which explore the relationships between the perimeter and area of a geometric figure, could be applied to this hexagon. This would involve finding the hexagon with the maximum area for a given perimeter or, conversely, the minimum perimeter for a given area. Solving such optimization problems adds another layer of complexity and necessitates advanced mathematical tools, potentially involving calculus of variations.
Conclusion: Unlocking the Secrets of a Unique Shape
The hexagon with exactly one pair of parallel sides, while seemingly simple, presents a rich and complex geometric challenge. Its unique properties, from the distribution of its internal angles to the challenges of calculating its area, require a deeper understanding of geometry and mathematical problem-solving. By exploring its construction, variations, and potential applications, we begin to unravel the secrets of this often-overlooked geometric shape. Its study not only enhances our geometrical understanding but also highlights the versatility and complexity inherent in seemingly simple shapes, emphasizing the power of mathematical exploration and problem-solving. Further investigation into specific cases and the use of advanced mathematical techniques promise to reveal even more fascinating aspects of this unique six-sided polygon. The journey of discovery continues, inviting further exploration into the captivating world of geometric shapes.
Latest Posts
Latest Posts
-
5 Letter Word With 3 Vowels And 2 Consonants
Jul 30, 2025
-
1 Lb Macaroni Is How Many Cups
Jul 30, 2025
-
How To Hand Sew Two Pieces Of Fabric Together
Jul 30, 2025
-
What Is 1 4 Cup 1 4 Cup
Jul 30, 2025
-
How Many Candy Corn In A Bag
Jul 30, 2025
Related Post
Thank you for visiting our website which covers about A Hexagon With Exactly 1 Pair Of Parallel Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.