A Negative Divided By A Positive Equals
Kalali
Apr 22, 2025 · 5 min read
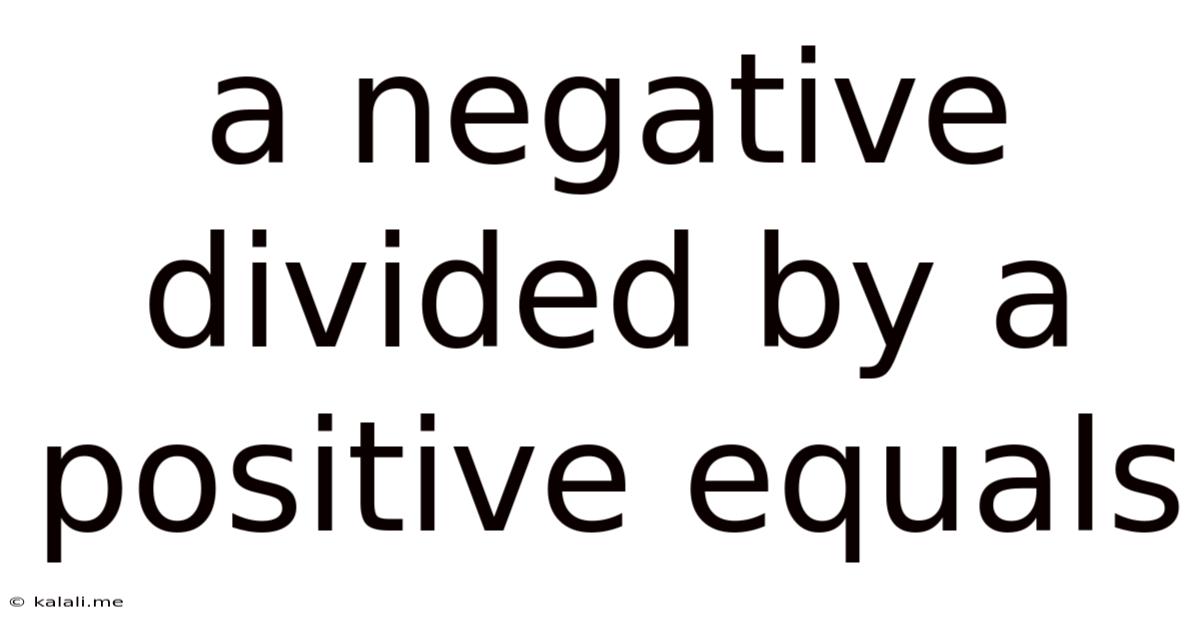
Table of Contents
A Negative Divided by a Positive Equals: Understanding the Rules of Division with Signed Numbers
Understanding the rules governing the division of signed numbers is crucial for mastering fundamental arithmetic and algebra. This comprehensive guide will delve into the intricacies of dividing negative and positive numbers, explaining the underlying principles and providing practical examples to solidify your understanding. We'll explore why a negative divided by a positive equals a negative, examining its application in various mathematical contexts and dispelling common misconceptions. This in-depth explanation is designed to leave you with a complete grasp of this essential mathematical concept.
Meta Description: Learn the definitive rules for dividing signed numbers. This guide explains why a negative divided by a positive equals a negative, providing examples and clarifying common misconceptions. Master this fundamental math concept today!
The Fundamental Principle: The Sign Rules
At the heart of understanding division with signed numbers lies the relationship between multiplication and division. They are inverse operations; division can be thought of as repeated subtraction, while multiplication is repeated addition. The sign rules for multiplication directly inform the sign rules for division. Remember the basic rules of multiplication with signed numbers:
- Positive × Positive = Positive
- Positive × Negative = Negative
- Negative × Positive = Negative
- Negative × Negative = Positive
Since division is the inverse of multiplication, these rules apply equally to division. Therefore:
- Positive ÷ Positive = Positive
- Positive ÷ Negative = Negative
- Negative ÷ Positive = Negative
- Negative ÷ Negative = Positive
This article will focus specifically on the rule: Negative ÷ Positive = Negative.
Visualizing Division: The Number Line Approach
One way to visualize the division of signed numbers is by using a number line. Let's consider the example of -6 ÷ 2 = -3. This can be interpreted as: "How many times can we subtract 2 from -6 to reach 0?"
- Start at -6 on the number line.
- Subtract 2: -6 - 2 = -8. We haven't reached 0 yet.
- It's more accurate to think of it as finding how many groups of 2 are in -6. We'll need three groups of 2 going to the negative direction to reach 0.
- We can represent this as three jumps of -2, to get from -6 to 0.
This visual representation reinforces the concept that dividing a negative number by a positive number results in a negative quotient. The number of groups (quotient) has a negative value.
Practical Applications: Real-World Examples
Understanding the division of signed numbers is essential for solving problems in various fields. Here are a few examples:
-
Finance: Imagine tracking your bank account. If you spend $20 (represented as -20) over 5 days, your average daily spending is -20 ÷ 5 = -$4. The negative sign indicates a decrease in your balance.
-
Temperature: If the temperature drops 12 degrees Celsius (-12°C) over 3 hours, the average hourly temperature drop is -12 ÷ 3 = -4°C. The negative sign shows a decrease in temperature.
-
Elevation: If a submarine descends 30 meters (-30m) over 10 minutes, its average descent rate is -30 ÷ 10 = -3 meters per minute. The negative indicates a downward movement.
-
Physics: In physics, negative values often represent direction or changes in direction. For example, if an object's velocity changes by -15 meters per second over 5 seconds, then it has experienced a deceleration of -15 ÷ 5 = -3 meters per second squared (m/s²). The negative value indicates that the object was slowing down.
Dispelling Common Misconceptions
A common source of confusion is the relationship between the absolute values of the numbers and the sign of the result. While the absolute value of -6 ÷ 2 is |-6 ÷ 2| = 3, the actual result of the division is -3. Focusing solely on the absolute values ignores the critical role of the signs in determining the overall sign of the result.
Another misconception is assuming that dividing a negative number always results in a negative number. This is incorrect. Dividing a negative number by another negative number yields a positive result. The sign of the result depends on the signs of both the dividend and the divisor.
Advanced Concepts and Applications
The principles of dividing signed numbers extend beyond basic arithmetic. Consider these advanced concepts:
-
Algebra: Solving algebraic equations often involves manipulating signed numbers. For example, solving the equation -2x = 6 requires dividing both sides by -2, resulting in x = -3.
-
Calculus: Derivatives and integrals frequently involve working with functions that may contain both positive and negative values. Understanding the rules of signed number division is crucial for accurately evaluating these functions.
-
Computer Programming: Computer programming relies heavily on arithmetic operations, including division with signed numbers. Understanding these rules is essential for writing accurate and efficient programs.
-
Statistics: Calculating means and standard deviations often involves working with both positive and negative data points, necessitating an understanding of signed number division.
-
Data Analysis: Many data sets involve both positive and negative values. Understanding the implications of division with signed numbers is vital for interpreting the data accurately and drawing valid conclusions.
Practice Problems
To reinforce your understanding, try these practice problems:
- -15 ÷ 5 = ?
- -24 ÷ -6 = ?
- 36 ÷ -9 = ?
- -50 ÷ 10 = ?
- -72 ÷ -8 = ?
Answers: 1. -3, 2. 4, 3. -4, 4. -5, 5. 9
These examples further illustrate the practical application and importance of understanding the rules for dividing signed numbers. Remember to always consider the signs of both the dividend and the divisor when determining the sign of the quotient.
Conclusion: Mastering Signed Number Division
Mastering the division of signed numbers is a cornerstone of mathematical proficiency. By understanding the underlying principles, visualizing the operation, and applying it to real-world scenarios, you can confidently tackle more complex mathematical problems. This guide has equipped you with the knowledge and tools to confidently perform and understand divisions involving negative and positive numbers, laying a strong foundation for future mathematical endeavors. Remember the key principle: a negative divided by a positive always equals a negative. Regular practice and application of these rules will solidify your understanding and improve your mathematical skills significantly.
Latest Posts
Latest Posts
-
Cuantos Pies Tiene Un Acre De Terreno
Apr 23, 2025
-
Cuantos Pies Hay En Una Milla
Apr 23, 2025
-
48 Inches Tall Is How Many Feet
Apr 23, 2025
-
What Is 7 Out Of 9
Apr 23, 2025
-
A Hair Salon Acquired 100 New Customers
Apr 23, 2025
Related Post
Thank you for visiting our website which covers about A Negative Divided By A Positive Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.