Are Alternate Interior Angles Always Congruent
Kalali
Mar 29, 2025 · 5 min read
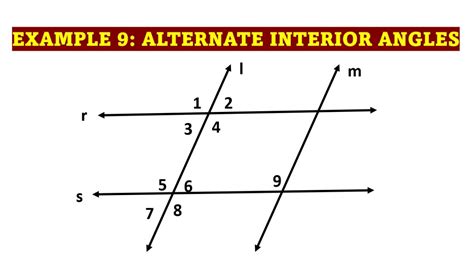
Table of Contents
Are Alternate Interior Angles Always Congruent? A Deep Dive into Geometry
Understanding the relationship between angles formed by intersecting lines is fundamental in geometry. A common topic of discussion, and sometimes confusion, involves alternate interior angles. The question at hand: are alternate interior angles always congruent? The short answer is: no, but under specific circumstances, they are. Let's delve into the specifics, exploring the conditions under which alternate interior angles are congruent and providing a comprehensive understanding of this geometric concept.
What are Alternate Interior Angles?
Before we address the core question, let's clearly define what alternate interior angles are. Consider two parallel lines intersected by a transversal line (a line that crosses both parallel lines). This intersection creates eight angles. Alternate interior angles are a pair of angles that:
- Lie on opposite sides of the transversal.
- Are located between the two parallel lines.
These angles are "alternate" because they are on opposite sides of the transversal and "interior" because they lie within the parallel lines.
Visual Representation:
Imagine two parallel lines, line m and line n, intersected by a transversal line, line t. The angles formed can be labeled as follows (using numbers for simplicity):
m
1|2
-----t-----
3|4
n
In this diagram, angles 3 and 6, and angles 4 and 5, are pairs of alternate interior angles.
The Parallel Postulate: The Key to Congruence
The congruence of alternate interior angles hinges on a crucial geometric postulate: the Parallel Postulate. This postulate states that given a line and a point not on the line, there exists exactly one line through the point that is parallel to the given line. This seemingly simple statement is the foundation for much of Euclidean geometry.
When two parallel lines are intersected by a transversal, the Parallel Postulate guarantees several angle relationships, including the congruence of alternate interior angles. This is only true if the lines are parallel. If the lines are not parallel, the alternate interior angles are not congruent.
Proving Alternate Interior Angles are Congruent (When Parallel)
We can formally prove the congruence of alternate interior angles using the Parallel Postulate and other geometric theorems. Here's a typical proof:
Given: Lines m and n are parallel, intersected by transversal t.
Prove: Alternate interior angles are congruent (e.g., ∠3 ≅ ∠6).
Proof:
- ∠3 and ∠1 are supplementary: They form a linear pair (angles on a straight line that add up to 180°).
- ∠1 and ∠6 are congruent: They are corresponding angles (angles in the same relative position at the intersection of two lines by a transversal, when lines are parallel).
- Therefore, ∠3 and ∠6 are supplementary: Since ∠3 and ∠1 are supplementary, and ∠1 ≅ ∠6, then ∠3 and ∠6 are supplementary.
- However, This isn't enough to prove congruence. This step highlights that while supplementary to a congruent angle does not automatically lead to congruence itself.
Revised Proof incorporating consecutive interior angles:
- ∠3 and ∠5 are consecutive interior angles: They are on the same side of the transversal and between the parallel lines.
- ∠3 and ∠5 are supplementary: Consecutive interior angles are supplementary when lines are parallel. This is a direct consequence of the parallel postulate.
- ∠5 and ∠6 are vertical angles: They are opposite angles formed by intersecting lines.
- ∠5 ≅ ∠6: Vertical angles are always congruent.
- Therefore, ∠3 ≅ ∠6: Since ∠3 and ∠5 are supplementary, and ∠5 ≅ ∠6, then by substitution, ∠3 and ∠6 are congruent.
This more robust proof leverages the relationship between consecutive interior angles and vertical angles to establish the congruence of alternate interior angles when the lines are parallel.
When Alternate Interior Angles are NOT Congruent
The crucial caveat is that the congruence of alternate interior angles is conditional. It only holds true when the two lines intersected by the transversal are parallel. If the lines are not parallel, the alternate interior angles will have different measures. The difference in their measures will depend on the angle between the non-parallel lines.
Illustrative Example:
Imagine two lines that intersect at an angle of 60°. A transversal line crossing both these lines will create alternate interior angles that are not congruent. The angles will reflect the angle of intersection of the two non-parallel lines.
Applications of Alternate Interior Angles
Understanding alternate interior angles has significant applications in various fields:
- Construction: Ensuring parallel walls and floors in buildings relies on the principles of alternate interior angles. Builders can use measurements of angles to verify the parallelism of structures.
- Engineering: Designing bridges and other structures requires precise calculations involving angles, and the concept of alternate interior angles plays a crucial role in ensuring stability and structural integrity.
- Cartography: Mapping and surveying involve determining distances and angles, with parallel lines often used as references. Understanding alternate interior angles helps in accurate calculations.
- Computer Graphics: In computer-aided design (CAD) and other graphics applications, the principles of alternate interior angles are crucial for creating accurate representations of objects and scenes. Parallel lines are frequently used in perspective drawing and modeling.
Common Mistakes and Misconceptions
A common mistake is assuming that alternate interior angles are always congruent, regardless of the lines' parallelism. This is incorrect. Remember, the parallelism of the lines is an essential prerequisite for the congruence of alternate interior angles.
Another misconception involves confusing alternate interior angles with other angle relationships, such as consecutive interior angles or corresponding angles. While all these angle relationships are relevant when dealing with parallel lines and transversals, they represent distinct geometric relationships with different properties. Clearly understanding each type of angle relationship is crucial.
Conclusion: Parallelism is Paramount
In conclusion, alternate interior angles are congruent only when the two lines intersected by the transversal are parallel. This condition is not optional; it's the fundamental basis of the relationship. The Parallel Postulate underpins this geometric property. Understanding this condition, and the proofs that demonstrate the relationship between parallel lines and alternate interior angles, is vital for mastering geometric principles and their applications in various fields. Remember to always carefully assess whether the lines in question are parallel before concluding that alternate interior angles are congruent. Failing to recognize this crucial condition can lead to significant errors in geometric calculations and problem-solving.
Latest Posts
Latest Posts
-
107 Cm Is How Many Inches
Apr 01, 2025
-
What Is One Percent Of A Billion
Apr 01, 2025
-
How Many Litres Is 24 Ounces
Apr 01, 2025
-
A Ray That Divides Two Congruent Angles
Apr 01, 2025
-
What Is A 14 Out Of 30
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Are Alternate Interior Angles Always Congruent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
