Area Rectangulo Circulo De Radio 8
Kalali
Apr 06, 2025 · 5 min read
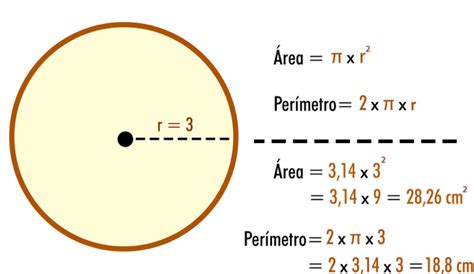
Table of Contents
Exploring the Area Relationships Between a Rectangle and a Circle with Radius 8
This article delves into the fascinating geometric relationships between a rectangle and a circle with a radius of 8 units. We will explore various scenarios, calculating areas, comparing sizes, and examining how changes in one shape's dimensions affect the other. We'll utilize mathematical principles to demonstrate the interplay between these two fundamental geometric figures.
Understanding the Fundamentals: Area Formulas
Before we embark on our exploration, let's refresh our understanding of the area formulas for rectangles and circles.
-
Rectangle: The area of a rectangle is calculated by multiplying its length (l) by its width (w). The formula is: Area = l * w
-
Circle: The area of a circle is determined by its radius (r). The formula is: Area = π * r², where π (pi) is approximately 3.14159.
In our case, the circle has a radius (r) of 8 units. Therefore, its area is:
Area = π * 8² = 64π ≈ 201.06 square units
Scenario 1: Rectangle Inscribed within a Circle
Imagine a rectangle perfectly inscribed within a circle of radius 8. This means that the corners of the rectangle touch the circumference of the circle. What is the maximum area this rectangle can have?
The maximum area occurs when the rectangle is a square. In this case, the diagonal of the square is equal to the diameter of the circle (2 * radius = 16 units). Using the Pythagorean theorem (a² + b² = c²), where 'a' and 'b' are the sides of the square and 'c' is the diagonal, we can find the side length (s) of the square:
s² + s² = 16² 2s² = 256 s² = 128 s = √128 ≈ 11.31 units
Therefore, the maximum area of a rectangle inscribed within a circle of radius 8 is approximately:
Area = s² = 128 square units.
This is significantly smaller than the area of the circle itself (approximately 201.06 square units). This demonstrates that even with optimal dimensions, a rectangle inscribed within a circle will always occupy a smaller area.
Scenario 2: Rectangle Circumscribing a Circle
Now, let's consider the opposite scenario: a rectangle circumscribing (surrounding) a circle of radius 8. The sides of the rectangle are tangent to the circle.
In this case, the width of the rectangle is equal to the diameter of the circle (2 * radius = 16 units). The length of the rectangle can vary. Let's assume, for simplicity, that the rectangle is also a square. Therefore, both the length and the width would be 16 units. The area of this square would be:
Area = 16 * 16 = 256 square units
This area is larger than the circle's area (approximately 201.06 square units), as expected. The relationship between the area of the circumscribing square and the circle showcases how the external shape can encompass a significantly larger area.
However, if we were to lengthen the rectangle while maintaining tangency to the circle, the area would increase. The area can be arbitrarily large depending on the length of the rectangle.
Scenario 3: Rectangle with Specific Dimensions
Let's analyze a rectangle with specific dimensions, for instance, a rectangle with a length of 12 units and a width of 10 units.
The area of this rectangle is simply:
Area = 12 * 10 = 120 square units
Comparing this area to the area of the circle (approximately 201.06 square units), we observe that the rectangle has a significantly smaller area. This highlights the dependence of the rectangle's area on its dimensions, illustrating that a rectangle does not always occupy less area compared to the circle. If the rectangle had dimensions of 20 units by 10 units, for instance, it would have an area larger than the circle.
Scenario 4: Exploring Area Ratios
The comparison of areas can be further analyzed by calculating area ratios. For instance, let's consider the ratio of the rectangle's area (in Scenario 1, the inscribed square) to the circle's area:
Ratio = Area of Inscribed Square / Area of Circle ≈ 128 / 201.06 ≈ 0.637
This ratio shows that the inscribed square occupies roughly 63.7% of the circle's area. This ratio remains constant regardless of the circle's radius, as long as it’s a square inscribed within the circle.
Different ratios will emerge when comparing the circle to other rectangles with varying dimensions. These ratios allow for a quantitative analysis of the relative sizes and highlight how the relationship between the rectangle and circle changes depending on the chosen rectangle dimensions.
Mathematical Implications and Further Explorations
The exploration of area relationships between a rectangle and a circle with a radius of 8 offers a multitude of opportunities for further investigation. We could:
-
Explore different inscribed shapes: Instead of rectangles, we could explore other shapes inscribed within the circle, such as triangles or ellipses, comparing their areas to the circle's area.
-
Introduce more complex relationships: Consider scenarios where the rectangle and circle are not perfectly aligned or where one shape is partially contained within the other.
-
Utilize calculus: Calculus can be used to determine the maximum or minimum areas under various constraints, such as fixed perimeters or areas.
-
Geometric proofs: Formal geometric proofs can be developed to rigorously establish the relationships observed.
Practical Applications
The concepts explored here have practical applications in various fields:
-
Engineering and Design: Understanding area relationships is crucial in designing structures, optimizing space utilization, and determining material requirements.
-
Computer Graphics: These calculations are fundamental in computer-aided design (CAD) software, game development, and other areas involving geometric representation.
-
Physics and Mathematics: The analysis of area relationships helps to model physical phenomena and solve geometric problems.
Conclusion
The analysis of the area relationships between a rectangle and a circle with a radius of 8 provides a rich and insightful exploration of fundamental geometric concepts. By applying simple formulas and logical reasoning, we can uncover fascinating relationships and appreciate the mathematical elegance inherent in these seemingly simple shapes. Furthermore, the practical applications of these calculations extend into many aspects of science, engineering, and design, highlighting the importance of understanding these geometric principles. The ability to calculate and compare areas accurately is a fundamental skill for problem-solving across various disciplines. This article serves as a starting point for deeper explorations into the intricate world of geometric relationships and their applications.
Latest Posts
Latest Posts
-
How Many Ft Is 96 Inches
Apr 09, 2025
-
What Is 13 15 As A Grade
Apr 09, 2025
-
Is A Kite Always A Quadrilateral
Apr 09, 2025
-
How Many Cups Are In 12 Gallons
Apr 09, 2025
-
Is Sulfur A Metal Or Nonmetal
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Area Rectangulo Circulo De Radio 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.