Common Multiples Of 4 And 14
Kalali
Apr 04, 2025 · 5 min read
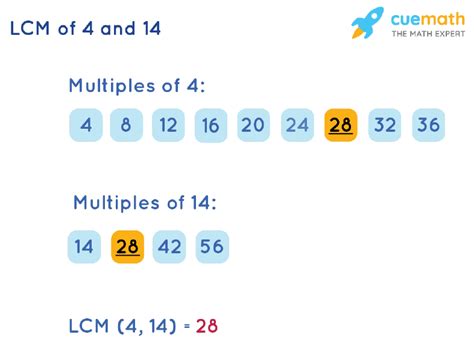
Table of Contents
Unveiling the Mysteries of Common Multiples: A Deep Dive into the Relationship Between 4 and 14
Finding common multiples, especially for seemingly simple numbers like 4 and 14, can seem straightforward. However, a deeper exploration reveals fascinating mathematical patterns and connections that extend far beyond basic arithmetic. This article delves into the world of common multiples, focusing specifically on the relationship between 4 and 14. We'll explore various methods for finding these multiples, uncover underlying mathematical principles, and even touch upon the practical applications of such concepts.
Understanding Common Multiples
Before we delve into the specifics of 4 and 14, let's establish a foundational understanding of common multiples. A multiple of a number is any number that results from multiplying that number by an integer (whole number). For example, multiples of 4 include 4, 8, 12, 16, 20, and so on. Similarly, multiples of 14 include 14, 28, 42, 56, 70, and so forth.
A common multiple is a number that is a multiple of two or more numbers. In our case, we're interested in the common multiples of 4 and 14. These are the numbers that appear in both the list of multiples of 4 and the list of multiples of 14.
Finding Common Multiples of 4 and 14: Method 1 - Listing Multiples
The most straightforward approach is to list the multiples of each number and identify the common ones.
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100...
Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140...
By comparing these lists, we can readily identify some common multiples: 28, 56, 84, and so on. This method works well for smaller numbers but becomes increasingly cumbersome as the numbers get larger.
Finding Common Multiples of 4 and 14: Method 2 - Prime Factorization
A more efficient and powerful method leverages the concept of prime factorization. Prime factorization involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 14: 2 x 7
To find the least common multiple (LCM), we take the highest power of each prime factor present in either factorization:
- LCM(4, 14): 2² x 7 = 28
The LCM is the smallest number that is a multiple of both 4 and 14. All other common multiples are multiples of the LCM. Therefore, the common multiples of 4 and 14 are multiples of 28: 28, 56, 84, 112, 140, and so on. This method is far more efficient for larger numbers where listing multiples becomes impractical.
Understanding the Least Common Multiple (LCM) and its Significance
The Least Common Multiple (LCM), as we've seen, plays a crucial role in identifying all common multiples. It's the smallest positive integer that is a multiple of both numbers. Understanding the LCM is vital in various mathematical contexts, including:
- Fraction addition and subtraction: Finding a common denominator is essential when adding or subtracting fractions. The LCM of the denominators serves as the least common denominator.
- Solving problems involving cycles: Imagine two gears rotating at different speeds. The LCM helps determine when both gears will simultaneously be at their starting position.
- Scheduling and planning: LCM is useful in scheduling events that occur at regular intervals, ensuring they align at certain points.
Exploring the Relationship Between 4 and 14: A Deeper Dive
The relationship between 4 and 14, while seemingly simple, reveals intriguing mathematical connections. Notice that 4 is a factor of 28 (4 x 7 = 28) and 14 is also a factor of 28 (14 x 2 = 28). The LCM, 28, acts as a bridge, highlighting their interconnectedness. This illustrates the fundamental principle that the LCM contains all the prime factors of both numbers, raised to their highest powers.
Beyond the Basics: Applications and Extensions
The concept of common multiples extends beyond simple number relationships. It forms the foundation for more advanced mathematical concepts, including:
- Modular arithmetic: Used extensively in cryptography and computer science, it involves operations on remainders after division. Understanding LCM is crucial in solving problems related to congruences and cyclic groups.
- Abstract algebra: The concepts of LCM and greatest common divisor (GCD) are generalized in abstract algebra, providing a framework for understanding structures like rings and ideals.
- Number theory: Advanced number theory utilizes concepts of LCM and GCD to explore properties of numbers, primes, and divisibility.
Practical Applications in Everyday Life
While seemingly abstract, the concept of common multiples has surprising practical applications in everyday life:
- Scheduling: Coordinating meeting schedules, bus routes, or even household chores involves finding common times or intervals, often implicitly using the LCM concept.
- Construction and design: In architecture and engineering, calculations related to structural elements, tiling patterns, or repeating designs often involve finding common multiples.
- Music theory: Musical intervals and chord progressions are based on ratios and multiples of frequencies, demonstrating the subtle presence of number theory in musical composition.
Conclusion: A Journey Through the World of Common Multiples
Our exploration of the common multiples of 4 and 14 has taken us beyond simple arithmetic. We’ve uncovered the power of prime factorization, the significance of the LCM, and its broader applications in mathematics and everyday life. Understanding these concepts isn't merely about memorizing formulas; it's about appreciating the underlying mathematical principles and recognizing their pervasive influence in various fields. By mastering the techniques of finding common multiples, we gain a deeper understanding of the intricate relationships between numbers and the elegant patterns that govern them. The seemingly simple question of "what are the common multiples of 4 and 14?" opens a door to a rich and rewarding exploration of the world of mathematics. This journey demonstrates the beauty and practicality of mathematical concepts, highlighting their relevance beyond the classroom. The principles discussed here can be easily adapted to finding common multiples of any two (or more) numbers, emphasizing the versatility and lasting value of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Cuanto Son 97 Grados Fahrenheit En Centigrados
Apr 11, 2025
-
Is Chromatin In Plant Or Animal Cells
Apr 11, 2025
-
How Many Inches Are 75 Cm
Apr 11, 2025
-
How Long Is 42 Inches In Feet
Apr 11, 2025
-
37 Degrees C Is What In Fahrenheit
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about Common Multiples Of 4 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.