Common Multiples Of 4 And 5
Kalali
Apr 01, 2025 · 5 min read
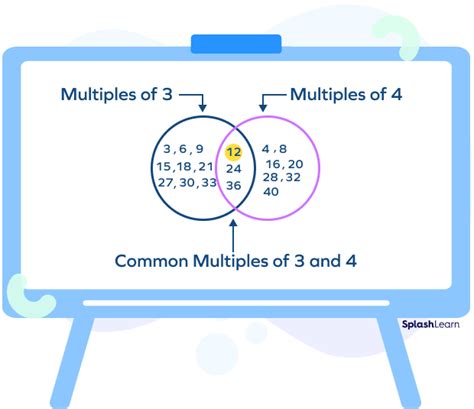
Table of Contents
Unveiling the Mysteries of Common Multiples of 4 and 5: A Deep Dive
Finding common multiples might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical elegance and practical applications. This comprehensive guide delves into the fascinating realm of common multiples, specifically focusing on the common multiples of 4 and 5. We'll explore their properties, methods for finding them, and even touch upon their relevance in various fields. Prepare to unlock a deeper appreciation for these seemingly simple numbers!
Understanding Multiples and Common Multiples
Before we embark on our journey into the specifics of 4 and 5, let's establish a solid foundation.
What are Multiples?
A multiple of a number is the result of multiplying that number by any whole number (0, 1, 2, 3, and so on). For example:
- Multiples of 4: 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40… and so on, extending infinitely.
- Multiples of 5: 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50… and so on, also extending infinitely.
Notice how each multiple is a product of the original number and a whole number.
What are Common Multiples?
Common multiples are numbers that are multiples of two or more numbers simultaneously. In other words, they appear in the lists of multiples for each of the numbers in question. For example, let's consider the numbers 4 and 5.
Some multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60… Some multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60…
Notice that 20, 40, and 60 appear in both lists. These are common multiples of 4 and 5.
Finding Common Multiples of 4 and 5: Methods and Techniques
There are several effective ways to identify common multiples of 4 and 5. Let's explore the most common methods:
1. Listing Multiples: A Simple Approach
The simplest method, especially for smaller numbers, is to list out the multiples of each number and then identify the common ones. As shown above, this method works well for visually identifying the smaller common multiples. However, it becomes less practical for larger numbers or when seeking higher common multiples.
2. Prime Factorization: A Powerful Technique
Prime factorization is a more sophisticated approach that provides a deeper understanding of the relationship between numbers. It involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 5: 5 (5 is a prime number)
To find the least common multiple (LCM), we take the highest power of each prime factor present in either number's factorization and multiply them together:
2² x 5 = 20
The LCM of 4 and 5 is 20. All other common multiples are multiples of the LCM. Therefore, the common multiples of 4 and 5 are 20, 40, 60, 80, 100, and so on.
3. Using the Formula: LCM and GCD
A more advanced approach uses the relationship between the Least Common Multiple (LCM) and the Greatest Common Divisor (GCD). The formula is:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the numbers (in our case, 4 and 5).
- GCD(a, b) is the greatest common divisor of a and b.
Since 4 and 5 have no common divisors other than 1, their GCD is 1. Therefore:
LCM(4, 5) = (4 x 5) / 1 = 20
This confirms that 20 is the least common multiple, and all other common multiples are multiples of 20.
Least Common Multiple (LCM) and its Significance
The least common multiple (LCM) holds particular importance in various mathematical contexts and real-world applications. For 4 and 5, the LCM is 20. This signifies:
- Smallest Common Multiple: It is the smallest positive integer that is a multiple of both 4 and 5.
- Foundation for Other Multiples: All other common multiples of 4 and 5 are multiples of 20 (20, 40, 60, 80...).
Real-World Applications of Common Multiples
Understanding common multiples isn't just an abstract mathematical exercise; it has practical applications in various fields:
1. Scheduling and Timing
Imagine you have two machines that operate on cycles: one every 4 hours and the other every 5 hours. To determine when they will operate simultaneously, you need to find the common multiples of 4 and 5. The first time they'll operate together is after 20 hours (the LCM).
2. Measurement and Conversion
Common multiples are crucial in converting units of measurement. For instance, converting inches to feet (12 inches = 1 foot) involves finding common multiples of the unit ratios.
3. Pattern Recognition and Sequences
Common multiples often underpin patterns and sequences in various mathematical and scientific domains, such as predicting cyclical phenomena.
4. Fraction Operations
Finding the common denominator when adding or subtracting fractions relies heavily on finding the LCM of the denominators. For example, to add 1/4 and 1/5, you would need to find the LCM of 4 and 5 (which is 20) to get a common denominator.
Exploring Further: Common Multiples Beyond 4 and 5
The principles and methods discussed above extend beyond the specific case of 4 and 5. You can apply these techniques to find common multiples of any set of numbers, regardless of their size or complexity. Remember that:
- Prime factorization remains a powerful tool for understanding the fundamental structure of numbers and finding LCMs efficiently.
- The LCM acts as a cornerstone, providing the basis for all other common multiples.
- Real-world applications are numerous and span various disciplines.
Conclusion: The Enduring Relevance of Common Multiples
The concept of common multiples, particularly exemplified by the exploration of common multiples of 4 and 5, reveals a fundamental aspect of number theory with practical implications far beyond the classroom. By mastering the techniques of finding LCMs and understanding their properties, you equip yourself with a valuable tool applicable to numerous mathematical and real-world problems. From scheduling tasks to performing fraction operations, the ability to identify and work with common multiples proves an invaluable asset across various fields. So, the next time you encounter a problem involving multiples, remember the power and elegance inherent in these seemingly simple mathematical concepts.
Latest Posts
Latest Posts
-
How Many Inches Is 183 Cm
Apr 02, 2025
-
What Is The Difference Between Basic Science And Applied Science
Apr 02, 2025
-
182 Inches Is How Many Feet
Apr 02, 2025
-
What Role Do Producers Play In The Ecosystem
Apr 02, 2025
-
What Is 192 Inches In Feet
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Common Multiples Of 4 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
