Consider The Differential Equation Given By Dy Dx Xy 2
Kalali
May 10, 2025 · 2 min read
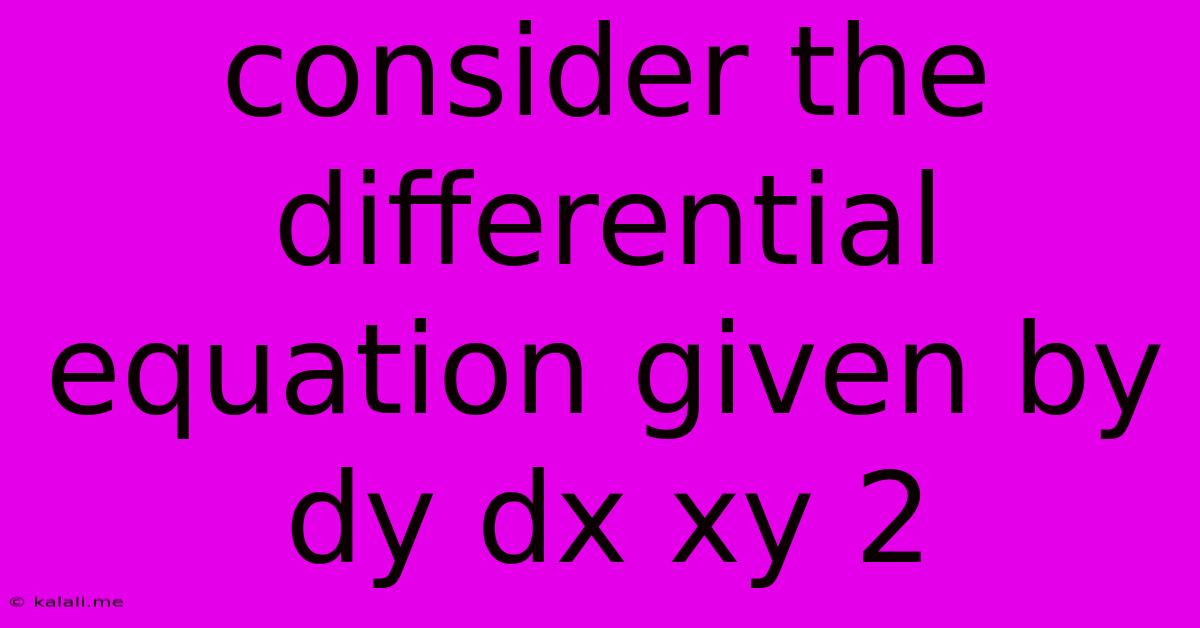
Table of Contents
Solving the Differential Equation dy/dx = xy²
This article explores the solution to the differential equation dy/dx = xy². This is a first-order, separable differential equation, meaning we can manipulate it to separate the variables x and y, allowing for straightforward integration. Understanding this type of equation is crucial in various fields, including physics, engineering, and economics, where modeling change over time is essential. Let's delve into the solution process step-by-step.
Understanding Separable Differential Equations
A separable differential equation is one that can be written in the form dy/dx = f(x)g(y), where f(x) is a function solely of x, and g(y) is a function solely of y. Our equation, dy/dx = xy², fits this form perfectly, with f(x) = x and g(y) = y².
Separating the Variables
The first step in solving a separable differential equation is to separate the variables. We achieve this by dividing both sides of the equation by y² (assuming y ≠ 0):
(1/y²) dy/dx = x
Now, multiply both sides by dx:
(1/y²) dy = x dx
Integrating Both Sides
With the variables separated, we can integrate both sides of the equation:
∫(1/y²) dy = ∫x dx
Performing the integration yields:
-1/y = (1/2)x² + C
where C is the constant of integration.
Solving for y
To express the solution explicitly in terms of y, we can manipulate the equation further:
-1/y = (x²/2) + C
Multiplying both sides by -1:
1/y = -(x²/2) - C
Taking the reciprocal of both sides:
y = 1 / (-(x²/2) - C)
We can simplify this expression by letting -C = K, where K is another arbitrary constant:
y = 1 / (-(x²/2) + K)
or equivalently:
y = 2 / (-x² + 2K)
This is the general solution to the differential equation dy/dx = xy². The constant K represents a family of solutions. Different values of K will result in different curves representing the solution.
Initial Conditions and Particular Solutions
The general solution contains an arbitrary constant, K. To find a particular solution, we need an initial condition – a point (x₀, y₀) that the solution must pass through. For example, if we were given that y(0) = 1, we could substitute x = 0 and y = 1 into our general solution to solve for K:
1 = 2 / (-(0)² + 2K)
This simplifies to 1 = 1/K, so K = 1. Therefore, the particular solution satisfying the initial condition y(0) = 1 is:
y = 2 / (-x² + 2)
Conclusion
Solving separable differential equations involves a systematic process of separating variables, integrating, and solving for the dependent variable. The solution obtained represents a family of curves, and specifying an initial condition allows us to identify a specific curve within that family. This methodology is fundamental to many applications requiring the analysis of rates of change. Remember to always consider the case where y=0 as it represents a singular solution that is not captured by the general solution derived above.
Latest Posts
Latest Posts
-
What Is The Average Iq For A 9 Year Old
Jul 13, 2025
-
How Long Does It Take For Brandy Melville To Ship
Jul 13, 2025
-
How Many Times Does 3 Go Into 30
Jul 13, 2025
-
In What Episode Of Bleach Does Ichigo Ask Orihime Out
Jul 13, 2025
-
How Much Is 4 Oz Chocolate Chips
Jul 13, 2025
Related Post
Thank you for visiting our website which covers about Consider The Differential Equation Given By Dy Dx Xy 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.