Definition Of Average Acceleration In Physics
Kalali
Apr 05, 2025 · 6 min read
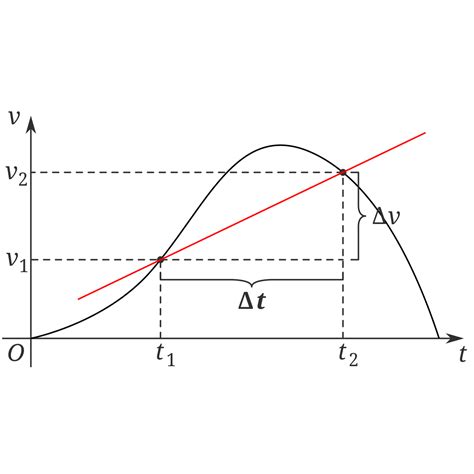
Table of Contents
Average Acceleration: A Deep Dive into Physics
Understanding acceleration is crucial for grasping the fundamentals of physics. While instantaneous acceleration describes the rate of change of velocity at a specific moment, average acceleration provides a broader picture, summarizing the overall change in velocity over a given time interval. This article will delve into the precise definition of average acceleration, explore its calculation, examine its applications, and discuss its relationship to other key concepts in physics.
What is Average Acceleration?
Average acceleration is a vector quantity that represents the overall change in velocity of an object divided by the total time taken for that change to occur. In simpler terms, it describes how much an object's velocity changes, on average, per unit of time. This is different from instantaneous acceleration, which considers the velocity change at a single point in time.
Definition:
Average acceleration (a<sub>avg</sub>) is defined mathematically as:
a<sub>avg</sub> = Δv / Δt
Where:
- Δv represents the change in velocity (final velocity - initial velocity). This is also a vector quantity, meaning it has both magnitude and direction.
- Δt represents the change in time (final time - initial time). This is a scalar quantity (only magnitude).
The units of average acceleration are typically meters per second squared (m/s²) in the SI system, but other units can be used depending on the context.
Understanding the Vector Nature of Acceleration
It's crucial to remember that velocity and acceleration are both vector quantities. This means they possess both magnitude (speed) and direction. A change in either speed or direction (or both) constitutes a change in velocity, resulting in acceleration. For example:
- A car speeding up in a straight line: This is a positive acceleration in the direction of motion.
- A car slowing down in a straight line: This is a negative acceleration (deceleration) in the direction of motion.
- A car turning at a constant speed: This is acceleration because the direction of velocity is changing, even though the speed remains constant. The acceleration is directed towards the center of the curve (centripetal acceleration).
Ignoring the vector nature of acceleration can lead to incorrect interpretations of motion.
Calculating Average Acceleration: Examples and Worked Problems
Let's illustrate the calculation of average acceleration with several examples:
Example 1: Linear Motion
A car accelerates from rest (0 m/s) to 20 m/s in 5 seconds. Calculate its average acceleration.
Solution:
- Initial velocity (v<sub>i</sub>) = 0 m/s
- Final velocity (v<sub>f</sub>) = 20 m/s
- Time interval (Δt) = 5 s
Δv = v<sub>f</sub> - v<sub>i</sub> = 20 m/s - 0 m/s = 20 m/s
a<sub>avg</sub> = Δv / Δt = 20 m/s / 5 s = 4 m/s²
The average acceleration of the car is 4 m/s².
Example 2: Change in Direction
A ball is thrown vertically upward with an initial velocity of 15 m/s. It reaches its highest point and then falls back down, reaching the same initial position after 3 seconds. Calculate the average acceleration of the ball.
Solution:
- Initial velocity (v<sub>i</sub>) = 15 m/s (upward)
- Final velocity (v<sub>f</sub>) = -15 m/s (downward – same speed, opposite direction)
- Time interval (Δt) = 3 s
Δv = v<sub>f</sub> - v<sub>i</sub> = -15 m/s - 15 m/s = -30 m/s
a<sub>avg</sub> = Δv / Δt = -30 m/s / 3 s = -10 m/s²
The average acceleration of the ball is -10 m/s². The negative sign indicates that the acceleration is directed downwards (due to gravity).
Example 3: More Complex Scenarios
Calculating average acceleration becomes more intricate when dealing with non-uniform acceleration (acceleration that changes over time). In such cases, graphical methods or calculus (using integrals) might be necessary. We'll explore these advanced techniques later.
Applications of Average Acceleration
Average acceleration finds widespread applications in various fields, including:
- Automotive Engineering: Determining the performance characteristics of vehicles, such as acceleration rates and braking performance.
- Aerospace Engineering: Analyzing the flight paths of aircraft and spacecraft, including takeoff, ascent, and descent phases.
- Sports Science: Evaluating the performance of athletes, such as measuring the acceleration of runners or swimmers.
- Physics Education: Serving as a foundational concept for understanding more complex motion scenarios.
- Robotics: Programming robots to move with specific accelerations, avoiding jerky movements.
Average Acceleration vs. Instantaneous Acceleration
While average acceleration provides a general overview of the change in velocity, instantaneous acceleration describes the acceleration at a precise moment in time. To find instantaneous acceleration, we need to consider the limit of the average acceleration as the time interval (Δt) approaches zero. This is represented mathematically using derivatives in calculus:
a<sub>instantaneous</sub> = dv/dt
This means the instantaneous acceleration is the derivative of velocity with respect to time. Graphically, the instantaneous acceleration at a given point on a velocity-time graph is represented by the slope of the tangent line at that point.
Average Acceleration and Graphs
Understanding how average acceleration relates to velocity-time graphs is crucial.
- Velocity-Time Graph: On a velocity-time graph, the average acceleration is represented by the slope of the secant line connecting the initial and final points of the time interval being considered.
- Constant Acceleration: If the acceleration is constant, the velocity-time graph will be a straight line, and the slope of this line represents the constant acceleration. The average acceleration and the instantaneous acceleration are identical in this case.
- Non-Constant Acceleration: If the acceleration is not constant, the velocity-time graph will be a curve. The average acceleration over a given time interval is still represented by the slope of the secant line, but the instantaneous acceleration at any point will be the slope of the tangent line at that point.
Analyzing these graphs provides a visual representation of the motion and helps understand the relationship between velocity and acceleration.
Advanced Concepts and Calculations
In scenarios involving non-uniform acceleration, the calculations become more complex. Here's how we might approach more sophisticated problems:
- Numerical Methods: For situations where an analytical solution is difficult to obtain, numerical methods such as finite difference approximations can be used to estimate average acceleration from discrete data points.
- Calculus (Integration): If the acceleration function a(t) is known as a function of time, the change in velocity can be determined by integrating the acceleration function over the time interval:
Δv = ∫a(t)dt
Similarly, the final velocity can be found by integrating the acceleration function and adding the initial velocity:
v<sub>f</sub> = v<sub>i</sub> + ∫a(t)dt
Conclusion
Average acceleration provides a fundamental tool for understanding the motion of objects, particularly in situations where a simpler, averaged representation is sufficient. While it may not capture the nuances of constantly changing acceleration, its simplicity and broad applicability make it an essential concept in physics, engineering, and many other fields. Understanding its definition, calculation, and relationship to other concepts, such as instantaneous acceleration and graphical representations, is key to mastering more complex motion problems. Remember to always consider the vector nature of velocity and acceleration for accurate analysis and interpretation.
Latest Posts
Latest Posts
-
What Is 9 In Fraction Form
Apr 05, 2025
-
Is 23 A Prime Or Composite
Apr 05, 2025
-
How Many Ml In 5 L
Apr 05, 2025
-
What Is 1 8 Oz In Grams
Apr 05, 2025
-
180 Ml Is How Many Cups
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Definition Of Average Acceleration In Physics . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
