Derivative Of X 2 X 1
Kalali
May 19, 2025 · 3 min read
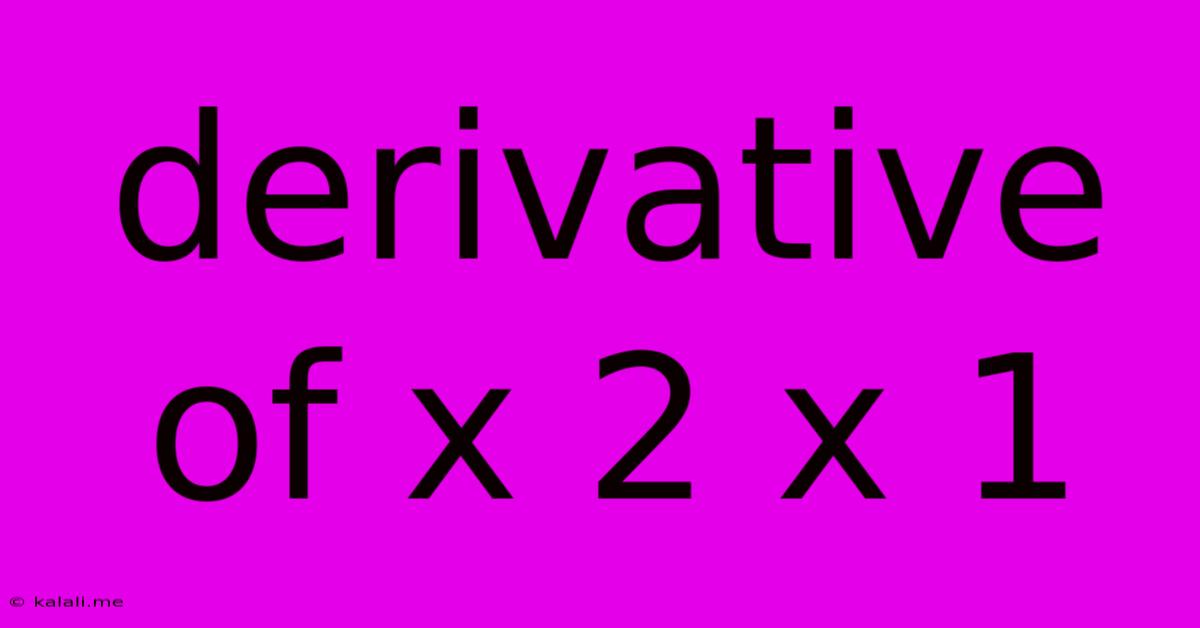
Table of Contents
Finding the Derivative of x² + x - 1: A Step-by-Step Guide
This article will guide you through the process of finding the derivative of the function f(x) = x² + x - 1. Understanding derivatives is fundamental in calculus and has wide-ranging applications in various fields, from physics and engineering to economics and finance. This tutorial will cover the basic rules of differentiation needed to solve this problem and provide a clear, step-by-step explanation.
Understanding Derivatives
Before we dive into the calculation, let's briefly review what a derivative represents. The derivative of a function at a point represents the instantaneous rate of change of the function at that point. Geometrically, it represents the slope of the tangent line to the function's graph at that point.
Rules of Differentiation
To find the derivative of x² + x - 1, we'll utilize two essential rules of differentiation:
-
The Power Rule: The derivative of xⁿ is nxⁿ⁻¹. This rule applies to any power of x, including those where n is a fraction or a negative number.
-
The Constant Rule: The derivative of a constant is 0. This means that the derivative of any number (like -1 in this case) is always zero.
Calculating the Derivative
Now, let's apply these rules to find the derivative of f(x) = x² + x - 1. We'll differentiate the function term by term:
-
Derivative of x²: Applying the power rule (n=2), the derivative of x² is 2x²⁻¹ = 2x.
-
Derivative of x: Applying the power rule (n=1), the derivative of x is 1x¹⁻¹ = 1.
-
Derivative of -1: Applying the constant rule, the derivative of -1 is 0.
Putting it Together
Combining the derivatives of each term, we get:
f'(x) = 2x + 1 + 0 = 2x + 1
Therefore, the derivative of x² + x - 1 is 2x + 1. This means that the instantaneous rate of change of the function f(x) at any point x is given by 2x + 1. For example, at x = 2, the instantaneous rate of change is 2(2) + 1 = 5.
Applications of Derivatives
Understanding and calculating derivatives is crucial for various mathematical operations and problem-solving. Some key applications include:
- Finding maximum and minimum values of functions: Setting the derivative equal to zero helps identify critical points where a function might reach a maximum or minimum.
- Analyzing the rate of change: Derivatives allow us to study how a quantity changes over time or with respect to another variable.
- Optimization problems: Derivatives are essential in solving optimization problems, where the goal is to find the best possible solution under certain constraints.
- Related rates problems: These problems involve finding the rate of change of one variable with respect to another when both are changing over time.
By mastering the fundamentals of differentiation, you open the door to a deeper understanding of calculus and its wide-ranging applications. This simple example of finding the derivative of x² + x - 1 provides a solid foundation for exploring more complex derivative problems in the future.
Latest Posts
Latest Posts
-
How Long Does Feta Last Once Opened
May 19, 2025
-
How Long Does Baileys Keep Unopened
May 19, 2025
-
The Pure And Simple Truth Is Rarely Pure And Never
May 19, 2025
-
Can You Cook Partially Frozen Chicken
May 19, 2025
-
How To Say How In French
May 19, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.