Describe The Cross Section Of The Rectangular Prism
Kalali
Apr 02, 2025 · 5 min read
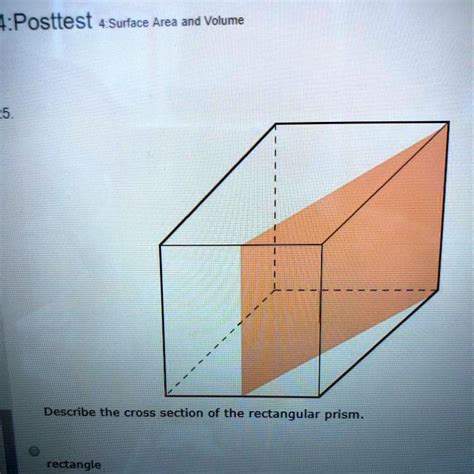
Table of Contents
Exploring the Cross Sections of a Rectangular Prism: A Comprehensive Guide
The rectangular prism, a ubiquitous three-dimensional shape found everywhere from building blocks to shipping containers, offers a fascinating exploration into the geometry of cross sections. Understanding how a plane intersects this solid reveals a wealth of geometrical concepts and shapes, ranging from the familiar to the more surprising. This article provides a comprehensive guide to understanding the cross sections of a rectangular prism, delving into various intersecting planes and the resulting shapes.
What is a Cross Section?
Before we dive into the specifics of rectangular prisms, let's define what a cross section is. A cross section is the two-dimensional shape formed by the intersection of a three-dimensional object and a plane. Imagine slicing through an object with a perfectly flat knife – the surface of the cut is the cross section. The shape of this cross section depends entirely on the orientation of the cutting plane relative to the 3D object.
The Rectangular Prism: A Foundation for Exploration
A rectangular prism is a three-dimensional shape with six rectangular faces, where opposite faces are congruent and parallel. It's also known as a cuboid, with cubes being a special case where all sides are equal. This seemingly simple shape provides a surprisingly diverse range of cross sections.
Exploring Different Cross Sections of a Rectangular Prism
The variety of cross sections achievable from a rectangular prism stems from the numerous ways a plane can intersect it. Let’s explore some common scenarios:
1. Rectangular Cross Sections: The Most Common Outcome
The most frequently observed cross section of a rectangular prism is, unsurprisingly, a rectangle. This occurs when the cutting plane is parallel to any of the faces of the prism. If the plane is parallel to a specific face, the resulting rectangle will be congruent to that face. Even slightly angled planes, as long as they don't intersect opposite edges simultaneously, will generally produce rectangles.
- Key takeaway: Parallel planes produce congruent cross sections. Slightly angled planes can also create rectangles, often smaller than the faces.
2. Square Cross Sections: A Special Case
If the rectangular prism is a cube, and the cutting plane is parallel to a face, the cross section will be a square. Even in a non-cubic rectangular prism, specific angles of the intersecting plane can create a square. This is less common than rectangles, but entirely possible.
- Key takeaway: A cube's parallel cross-sections are squares, while non-cubic prisms need precise plane orientations to create square cross-sections.
3. Parallelogram Cross Sections: Introducing Angles
When the intersecting plane is not parallel to any face, but still intersects only one pair of opposite faces, the resulting cross section will be a parallelogram. This is a quadrilateral with opposite sides parallel. The parallelogram will only be a rectangle if the plane intersects the prism perpendicularly.
- Key takeaway: Angled planes intersecting only opposite faces produce parallelograms. Their dimensions depend on the angle of the plane.
4. Triangular Cross Sections: The Most Complex Case
The most complex cross sections arise when the intersecting plane intersects more than two faces of the prism. In this scenario, the cross section becomes a triangle. This requires careful consideration of the plane's angle to the faces. The triangle can be an equilateral triangle, an isosceles triangle, or a scalene triangle, depending on the orientation of the plane.
- Key takeaway: Achieving triangular cross sections requires the plane to intersect at least three faces, resulting in varied types of triangles depending on the angle of the cut.
5. Trapezoidal Cross Sections: A Less Common Shape
Under specific conditions, a trapezoid can also be formed as a cross section. This happens when the cutting plane intersects two pairs of opposite faces, but doesn't intersect in such a way as to create a parallelogram or triangle. The trapezoid is a quadrilateral with at least one pair of parallel sides.
- Key takeaway: Carefully angled planes intersecting two pairs of opposite faces can create trapezoids. The angles are crucial to determining the type of trapezoid.
Visualizing the Cross Sections: Practical Applications
Understanding cross sections is not merely an academic exercise; it has numerous real-world applications. Consider these examples:
-
Construction and Engineering: Architects and engineers routinely utilize cross-sectional views to understand the internal structure of buildings, bridges, and other large-scale structures. Understanding how materials are arranged internally, based on different cross sections, is critical for structural integrity and design.
-
Medical Imaging: Medical scans like CT scans and MRI scans effectively create cross-sectional images of the human body. These allow doctors to visualize internal organs and tissues, aiding in diagnosis and treatment planning. Understanding cross sections is crucial for interpreting these images.
-
Manufacturing and Design: In manufacturing, cross-sectional diagrams are essential for understanding the internal structures of manufactured parts and designing intricate components. It is fundamental for ensuring consistent quality and design.
-
Geology: Geologists use cross-sectional diagrams to represent layers of rock and soil. This helps them understand geological formations, identify resources, and assess the risk of natural disasters. Visualizing different layers is essential.
Advanced Concepts and Further Exploration
The exploration of cross sections doesn't end with the rectangular prism. Expanding this knowledge opens doors to understanding cross sections of more complex three-dimensional shapes like:
-
Cylinders: Cross sections can range from circles (parallel to the base) to ellipses (non-parallel cuts) to rectangles (perpendicular cuts).
-
Cones: Cross sections can be circles, ellipses, triangles, and parabolas, depending on the cutting plane’s orientation.
-
Spheres: All cross sections of a sphere are circles.
Understanding these various cross-sections across different three-dimensional shapes enhances our ability to visualize and interpret complex structures and geometries.
Conclusion: Mastering the Art of Cross Sections
Mastering the concept of cross sections is a valuable skill that bridges the gap between two-dimensional representations and three-dimensional realities. The rectangular prism, although seemingly simple, provides a fantastic foundation for understanding these principles. By carefully considering the orientation of the intersecting plane and its relationship to the prism's faces, you can predict and understand the resulting two-dimensional shapes. This knowledge extends beyond academic studies and proves essential in various practical fields, from engineering and medicine to geology and manufacturing. Further exploration of cross sections in more complex shapes unlocks a deeper appreciation for geometry and spatial reasoning. The seemingly simple act of slicing through a shape reveals a surprising wealth of geometric possibilities.
Latest Posts
Latest Posts
-
How Many Mm Is 11 Cm
Apr 03, 2025
-
1 Meter 55 Cm In Feet
Apr 03, 2025
-
How Many Centimeters Are In 39 Millimeters
Apr 03, 2025
-
4 Over 3 As A Decimal
Apr 03, 2025
-
How Much Is 1 1 2 Cups
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Describe The Cross Section Of The Rectangular Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
