Describe The Main Parts Of A Proof
Kalali
Apr 01, 2025 · 6 min read
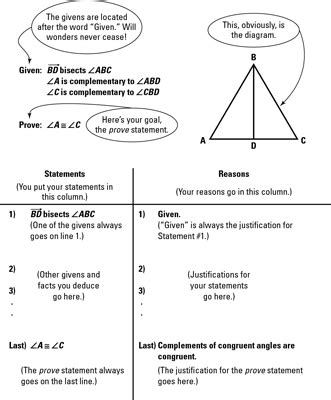
Table of Contents
Decoding the Main Parts of a Proof: A Comprehensive Guide
Mathematical proofs, the bedrock of mathematical certainty, often appear daunting at first glance. However, understanding their fundamental structure and common elements significantly reduces their complexity. This comprehensive guide delves into the main parts of a proof, equipping you with the knowledge to both understand and construct rigorous arguments. We'll explore various proof techniques, common pitfalls, and strategies to improve your proof-writing skills.
Understanding the Foundation: What is a Proof?
Before dissecting the parts, let's define what a proof actually is. A proof is a logical argument that establishes the truth of a statement, known as a theorem or proposition. This argument proceeds from previously established statements (axioms, definitions, or previously proven theorems) using logical rules of inference. The goal is to create an undeniable chain of reasoning, leading inexorably to the conclusion. Think of it as a meticulously constructed bridge, connecting known facts to the statement you aim to prove.
The Key Components of a Well-Structured Proof
A well-structured proof typically contains the following essential elements:
1. Statement of the Theorem (or Proposition):
This is the first and arguably the most important part. Clearly and concisely state the theorem you intend to prove. Ambiguity here can lead to confusion and invalidate the entire proof. The statement should include all necessary hypotheses (conditions that must be true) and the conclusion (the statement being proven). For example:
Theorem: If n is an even integer, then n² is an even integer.
This clearly states both the hypothesis (n is an even integer) and the conclusion (n² is an even integer).
2. Definitions and Assumptions:
Before diving into the argument, clearly define any terms or concepts crucial to the proof. This ensures that everyone understands the meaning of the terms being used, preventing misinterpretations. Explicitly state any assumptions being made. This sets the groundwork for the logical steps that follow.
For instance, in the above theorem, defining "even integer" as an integer divisible by 2 is crucial.
3. The Argument (Proof Body):
This is the core of the proof. It's a step-by-step logical progression from the hypotheses to the conclusion. Each step must be justified by a previously established fact (axiom, definition, or previously proven theorem) or a logical rule of inference. Common logical rules include:
- Modus Ponens: If P, then Q. P. Therefore, Q.
- Modus Tollens: If P, then Q. Not Q. Therefore, not P.
- Syllogism: If P, then Q. If Q, then R. Therefore, if P, then R.
The argument should be clear, concise, and easy to follow. Avoid unnecessary jargon or overly complex sentences. Using clear and precise language enhances readability and reduces the risk of errors.
4. Conclusion:
The final step explicitly restates the theorem and declares its proof. It should concisely summarize the outcome of the argument, reaffirming that the conclusion has been reached logically from the hypotheses.
For example: "Therefore, we have shown that if n is an even integer, then n² is an even integer."
Common Proof Techniques
Several techniques are commonly employed in constructing proofs. The choice of technique depends on the nature of the theorem being proven. Here are a few:
1. Direct Proof:
This is the most straightforward approach. Starting from the hypotheses, you directly apply logical rules and previously known facts to deduce the conclusion. The even integer theorem example above can be proven directly.
2. Proof by Contradiction (Reductio ad Absurdum):
This method starts by assuming the negation of the conclusion. Then, you proceed logically until you reach a contradiction (a statement that is both true and false). Since a contradiction is impossible within a consistent system, the initial assumption (the negation of the conclusion) must be false, thus proving the original conclusion.
For example, proving the irrationality of the square root of 2 often uses proof by contradiction.
3. Proof by Induction:
This technique is particularly useful for proving statements about integers. It involves two steps:
- Base Case: Prove the statement is true for a specific base value (usually 1 or 0).
- Inductive Step: Assume the statement is true for some arbitrary integer k, and then prove that it must also be true for k+1. This shows that if the statement is true for one integer, it must be true for the next, creating a chain reaction of truth extending to all integers greater than or equal to the base case.
4. Proof by Cases:
This method breaks the proof into several cases, where each case covers a specific sub-situation. By proving the conclusion for each case, you establish the overall truth of the theorem. This is often used when dealing with statements containing conditional statements or inequalities.
5. Proof by Exhaustion:
This technique is suitable for theorems with a finite number of cases. You explicitly prove the conclusion for each case. While effective for a small number of cases, it becomes impractical for larger sets.
Improving Your Proof-Writing Skills
Writing effective proofs requires practice and attention to detail. Here are some tips to enhance your proof-writing skills:
- Understand the Definitions: Thoroughly grasp the definitions of all terms involved. A misunderstanding of a definition can easily derail an entire proof.
- Practice Regularly: Consistent practice is key. Work through various examples and problems, focusing on different proof techniques.
- Break Down Complex Statements: For intricate proofs, break down the statement into smaller, more manageable parts. This simplifies the task and makes the logical progression clearer.
- Review and Revise: Once you have completed a proof, review it carefully. Check for any logical gaps, inconsistencies, or ambiguities. Revise your work to ensure clarity and correctness.
- Seek Feedback: Share your proofs with peers or instructors and solicit their feedback. This can help identify weaknesses and improve your understanding.
- Read Existing Proofs: Study well-written proofs to understand how experienced mathematicians structure their arguments. Pay attention to their style, clarity, and use of logical steps.
Common Pitfalls to Avoid
Several common errors can invalidate a proof. Be mindful of these pitfalls:
- Circular Reasoning: Using the conclusion as a premise to prove itself.
- Assuming the Conclusion: Implicitly assuming what you are trying to prove.
- Incorrect Logical Steps: Making faulty inferences or using incorrect logical rules.
- Vague or Ambiguous Language: Using unclear language that obscures the logical progression.
- Overlooking Special Cases: Failing to consider exceptional situations or boundary conditions.
Conclusion: Mastering the Art of Proof
Mastering the art of proof-writing is a journey that requires dedication, practice, and a deep understanding of logic and mathematics. By understanding the key parts of a proof, utilizing various proof techniques, and avoiding common pitfalls, you can construct rigorous, clear, and convincing arguments. Remember that a well-written proof is not only correct but also readily comprehensible, allowing others to follow your reasoning and appreciate the elegance of mathematical logic. The effort invested in developing these skills will greatly benefit your mathematical understanding and problem-solving abilities. Continuously refining your skills through practice and feedback will ultimately lead to a deep appreciation for the beauty and power of mathematical proof.
Latest Posts
Latest Posts
-
How Much Older Is John The Baptist Than Jesus
Jul 12, 2025
-
How Many Teaspoons In A Pound Of Sugar
Jul 12, 2025
-
How Do You Pass Level 12 On Bloxorz
Jul 12, 2025
-
How Far Is 0 4 Miles To Walk
Jul 12, 2025
-
What Is 20 Percent Of 800 000
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about Describe The Main Parts Of A Proof . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.