Distance Between Two Points In Polar Coordinates
Kalali
Apr 06, 2025 · 5 min read
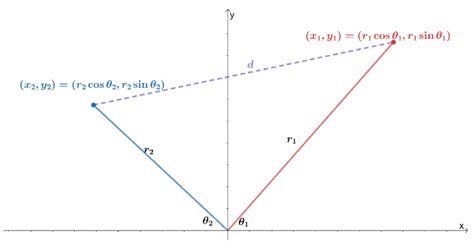
Table of Contents
Calculating the Distance Between Two Points in Polar Coordinates
Determining the distance between two points is a fundamental concept in geometry and has widespread applications across various fields, including physics, engineering, and computer graphics. While calculating this distance is straightforward in Cartesian coordinates (using the Pythagorean theorem), the process becomes slightly more involved when dealing with polar coordinates. This article provides a comprehensive guide to understanding and calculating the distance between two points expressed in polar coordinates, along with practical examples and applications.
Understanding Polar Coordinates
Before diving into the distance calculation, let's briefly review polar coordinates. Unlike Cartesian coordinates (x, y) which represent a point's position relative to the origin using horizontal and vertical distances, polar coordinates (r, θ) represent a point's position using its distance from the origin (r, the radial distance) and the angle (θ, the polar angle) it makes with the positive x-axis. The angle θ is typically measured counter-clockwise from the positive x-axis.
Converting Between Cartesian and Polar Coordinates
It's often useful to convert between Cartesian and polar coordinate systems. The conversion formulas are:
-
Cartesian to Polar:
r = √(x² + y²)θ = arctan(y/x)(Note: Consider the quadrant to determine the correct angle)
-
Polar to Cartesian:
x = r * cos(θ)y = r * sin(θ)
These conversion formulas are crucial for solving distance problems where points are given in different coordinate systems.
Calculating the Distance Using the Law of Cosines
The most straightforward method for finding the distance between two points (r₁, θ₁) and (r₂, θ₂) in polar coordinates involves using the Law of Cosines. Imagine these two points and the origin as the vertices of a triangle. The lengths of two sides of this triangle are r₁ and r₂, and the angle between them is |θ₂ - θ₁|. The Law of Cosines states:
d² = r₁² + r₂² - 2r₁r₂cos(|θ₂ - θ₁|)
where:
dis the distance between the two points.r₁andr₂are the radial distances of the two points.θ₁andθ₂are the polar angles of the two points.|θ₂ - θ₁|represents the absolute difference between the two angles.
This formula directly calculates the square of the distance. To find the distance itself, simply take the square root:
d = √(r₁² + r₂² - 2r₁r₂cos(|θ₂ - θ₁|))
Example Calculation
Let's consider two points: (r₁, θ₁) = (3, π/4) and (r₂, θ₂) = (5, π/2).
-
Calculate |θ₂ - θ₁|: |π/2 - π/4| = π/4
-
Substitute values into the Law of Cosines formula:
d² = 3² + 5² - 2 * 3 * 5 * cos(π/4)d² = 9 + 25 - 30 * (√2/2)d² = 34 - 15√2d² ≈ 34 - 21.21 ≈ 12.79 -
Take the square root to find the distance:
d ≈ √12.79 ≈ 3.576
Therefore, the distance between the points (3, π/4) and (5, π/2) is approximately 3.576 units.
Calculating the Distance Using Cartesian Conversion
Alternatively, you can convert both polar coordinates to Cartesian coordinates using the formulas mentioned earlier, then apply the Pythagorean theorem to find the distance.
-
Convert Polar to Cartesian: Convert (r₁, θ₁) and (r₂, θ₂) to their respective Cartesian coordinates (x₁, y₁) and (x₂, y₂).
-
Apply the Pythagorean Theorem: The distance 'd' between (x₁, y₁) and (x₂, y₂) is given by:
d = √((x₂ - x₁)² + (y₂ - y₁)²)
This method is equally valid and might be preferred if you already have the tools or software to handle Cartesian coordinate calculations readily.
Example using Cartesian Conversion
Let's use the same points as before: (r₁, θ₁) = (3, π/4) and (r₂, θ₂) = (5, π/2).
-
Convert to Cartesian:
- (x₁, y₁) = (3cos(π/4), 3sin(π/4)) = (3√2/2, 3√2/2)
- (x₂, y₂) = (5cos(π/2), 5sin(π/2)) = (0, 5)
-
Apply the Pythagorean Theorem:
d = √((0 - 3√2/2)² + (5 - 3√2/2)²)d = √((9*2/4) + (25 - 15√2 + 9*2/4))d = √(18/4 + 25 -15√2 + 18/4)d = √(34 - 15√2)d ≈ 3.576
As you can see, both methods yield the same result.
Applications of Distance Calculation in Polar Coordinates
The ability to calculate distances in polar coordinates is crucial in numerous applications:
1. Robotics and Navigation:
Robot navigation systems frequently use polar coordinates to represent the robot's position and the locations of obstacles. Calculating distances between the robot and obstacles or target points is essential for path planning and collision avoidance.
2. GPS and Location-Based Services:
GPS systems utilize latitude and longitude, which can be considered a spherical polar coordinate system. Calculating distances between locations on the Earth's surface requires adaptations of the distance formulas to account for the Earth's curvature.
3. Radar and Sonar Systems:
Radar and sonar systems detect objects by measuring their distance (range) and angle (bearing). The data obtained is naturally in polar coordinates, and distance calculations are crucial for target tracking and identification.
4. Computer Graphics and Game Development:
Many game engines and graphics programs use polar coordinates for representing object positions and orientations. Calculating distances between game characters or objects is crucial for collision detection, gameplay mechanics, and visual rendering.
5. Astronomy and Astrophysics:
Astronomical observations often involve measuring the position of celestial objects using their angular separation and distance from Earth. Calculating distances between stars and galaxies is fundamental to understanding the structure and evolution of the universe.
6. Signal Processing and Communications:
In signal processing and telecommunications, polar coordinates are used to represent signals in the frequency domain. Distance calculations can be relevant in tasks such as signal filtering and channel equalization.
Handling Special Cases and Considerations
While the Law of Cosines provides a general solution, some special cases deserve attention:
-
Points with the same radial distance: If r₁ = r₂, the formula simplifies to:
d = 2r₁sin(|θ₂ - θ₁|/2) -
Points with the same angle: If θ₁ = θ₂, the formula simplifies to:
d = |r₂ - r₁|(This is simply the difference in radial distances). -
Computational Accuracy: When dealing with very small or very large values of r₁ and r₂, it's essential to consider potential rounding errors during the calculation. Using high-precision arithmetic might be necessary in certain applications.
Conclusion
Calculating the distance between two points in polar coordinates is a valuable skill with widespread applications. Whether using the Law of Cosines directly or converting to Cartesian coordinates, understanding the different methods allows you to choose the most appropriate approach for your specific problem. Remembering the underlying geometry and considering potential special cases ensures accurate and efficient computations in various fields. By mastering these techniques, you'll be better equipped to solve complex problems involving spatial relationships in polar coordinate systems.
Latest Posts
Latest Posts
-
What Is Half Of 1 4 Teaspoon
Jul 02, 2025
-
How Many Cups In A Pound Of Hamburger Meat
Jul 02, 2025
-
Imagery Or Figurative Language From Romeo And Juliet
Jul 02, 2025
-
What Is A Quarter Of A Million
Jul 02, 2025
-
Which Of The Following Is True Concerning A Dao
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about Distance Between Two Points In Polar Coordinates . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.