Distance Between Two Points Polar Coordinates
Kalali
Apr 05, 2025 · 5 min read
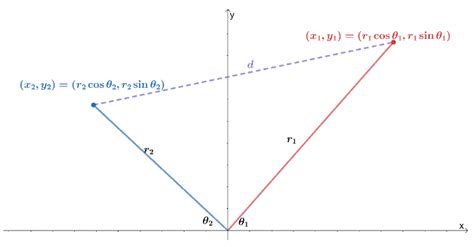
Table of Contents
Calculating the Distance Between Two Points in Polar Coordinates
Determining the distance between two points is a fundamental concept in geometry and has numerous applications across various fields, from physics and engineering to computer graphics and geographic information systems (GIS). While Cartesian coordinates (x, y) provide a straightforward approach to distance calculation using the Pythagorean theorem, the process becomes slightly more intricate when dealing with polar coordinates (r, θ). This article delves into the methods for calculating the distance between two points represented in polar coordinates, exploring both the direct derivation using the law of cosines and a conversion approach leveraging the Cartesian coordinate system. We will also examine specific scenarios and potential pitfalls, equipping you with a comprehensive understanding of this essential geometric calculation.
Understanding Polar Coordinates
Before diving into the distance calculation, let's briefly review the basics of polar coordinates. Instead of using perpendicular x and y axes, polar coordinates define a point's location using two values:
- r (radius): The distance of the point from the origin (0, 0). This is always a non-negative value.
- θ (theta): The angle (in radians or degrees) between the positive x-axis and the line segment connecting the origin to the point. The angle is typically measured counter-clockwise from the positive x-axis.
Therefore, a point is represented as (r, θ).
Method 1: Direct Calculation using the Law of Cosines
This method directly utilizes the geometric relationship between the two points and the origin, employing the law of cosines. Let's consider two points: P₁ (r₁, θ₁) and P₂ (r₂, θ₂). We want to find the distance 'd' between these two points.
The law of cosines states: c² = a² + b² - 2ab cos(C)
In our context:
- a = r₁
- b = r₂
- C = |θ₂ - θ₁| (the absolute difference between the angles; we use the absolute value to ensure a positive angle)
- c = d (the distance we want to calculate)
Substituting these values into the law of cosines, we get:
d² = r₁² + r₂² - 2r₁r₂ cos(|θ₂ - θ₁|)
To find the distance 'd', we take the square root:
d = √(r₁² + r₂² - 2r₁r₂ cos(|θ₂ - θ₁|))
This formula directly calculates the distance between two points in polar coordinates without any coordinate transformations. It's an elegant and efficient solution.
Method 2: Conversion to Cartesian Coordinates
Alternatively, we can convert the polar coordinates to Cartesian coordinates and then use the standard distance formula for Cartesian points. The conversion formulas are:
- x = r cos(θ)
- y = r sin(θ)
For point P₁ (r₁, θ₁):
- x₁ = r₁ cos(θ₁)
- y₁ = r₁ sin(θ₁)
For point P₂ (r₂, θ₂):
- x₂ = r₂ cos(θ₂)
- y₂ = r₂ sin(θ₂)
Now, we can use the distance formula for Cartesian coordinates:
d = √((x₂ - x₁)² + (y₂ - y₁)²)
Substituting the expressions for x₁, y₁, x₂, and y₂, we get:
d = √((r₂ cos(θ₂) - r₁ cos(θ₁))² + (r₂ sin(θ₂) - r₁ sin(θ₁))²)
While this method might seem longer, it provides a familiar approach for those comfortable with Cartesian coordinate calculations. It's also beneficial if other calculations involving Cartesian coordinates are already part of the problem.
Comparing the Two Methods
Both methods are perfectly valid for calculating the distance between two points in polar coordinates. The choice often depends on personal preference and the context of the problem:
-
Method 1 (Law of Cosines): This method is generally more efficient and direct, especially if you only need to calculate the distance. It avoids unnecessary conversions.
-
Method 2 (Cartesian Conversion): This approach is beneficial if you are already working with Cartesian coordinates or if other calculations necessitate the conversion to the Cartesian system. It might be easier to understand for those less familiar with the law of cosines.
Illustrative Examples
Let's solidify our understanding with a few examples:
Example 1:
Find the distance between P₁ (2, π/4) and P₂ (3, π/2).
Using Method 1 (Law of Cosines):
d = √(2² + 3² - 2 * 2 * 3 * cos(|π/2 - π/4|)) = √(4 + 9 - 12 * cos(π/4)) ≈ √(13 - 12 * 0.707) ≈ √(4.124) ≈ 2.03
Using Method 2 (Cartesian Conversion):
x₁ = 2 cos(π/4) = √2 y₁ = 2 sin(π/4) = √2 x₂ = 3 cos(π/2) = 0 y₂ = 3 sin(π/2) = 3
d = √((0 - √2)² + (3 - √2)²) ≈ √(2 + (3 - 1.414)² ) ≈ √(2 + 2.429) ≈ 2.03
Example 2:
Calculate the distance between P₁ (1, 0) and P₂ (1, π).
Using Method 1 (Law of Cosines):
d = √(1² + 1² - 2 * 1 * 1 * cos(|π - 0|)) = √(2 - 2 * cos(π)) = √(2 - 2 * -1) = √4 = 2
Using Method 2 (Cartesian Conversion): This example would yield the same result.
Handling Special Cases
-
Zero Radius: If either r₁ or r₂ is zero, the distance is simply the other radius. The point with a zero radius is located at the origin.
-
Identical Angles: If θ₁ = θ₂, the points lie on the same radial line, and the distance is simply |r₂ - r₁|.
-
Negative Radius: While conventionally, 'r' is non-negative, some systems might allow negative radii, representing the point on the opposite side of the origin. In such cases, you need to adjust the calculations accordingly, potentially considering the absolute value of the radius.
-
Angle Units: Ensure consistency in angle units (radians or degrees) throughout the calculation. Most mathematical functions expect radians; appropriate conversion is necessary if using degrees.
Applications
The ability to calculate distances in polar coordinates has broad applications:
- Robotics: Calculating distances between robot arms and objects.
- Radar systems: Determining the range and bearing of objects.
- Navigation systems: Calculating distances between geographic locations represented using polar coordinates.
- Physics: Modeling projectile motion, or calculations involving circular or rotational motion.
- Computer graphics: Calculating distances in game development or animation.
Conclusion
Calculating the distance between two points in polar coordinates involves either a direct application of the law of cosines or a conversion to Cartesian coordinates. Both methods are valid and offer different advantages depending on the specific problem and context. Understanding the underlying principles and potential special cases will equip you to effectively utilize either approach and successfully solve a wide range of geometric problems. Remember to always maintain consistency in your units (radians or degrees) to ensure accurate results. Mastering this calculation empowers you to tackle more advanced problems in various scientific and engineering disciplines.
Latest Posts
Latest Posts
-
Which Word Has The Most Positive Connotation
Jul 15, 2025
-
How Do I Send An Evite Reminder
Jul 15, 2025
-
When Performing A Self Rescue When Should You Swim To Shore
Jul 15, 2025
-
How Many Decaliters Are In A Liter
Jul 15, 2025
-
What Note Sits In The Middle Of The Grand Staff
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about Distance Between Two Points Polar Coordinates . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.