Divide 30 By Half And Add 10
Kalali
Aug 19, 2025 · 4 min read
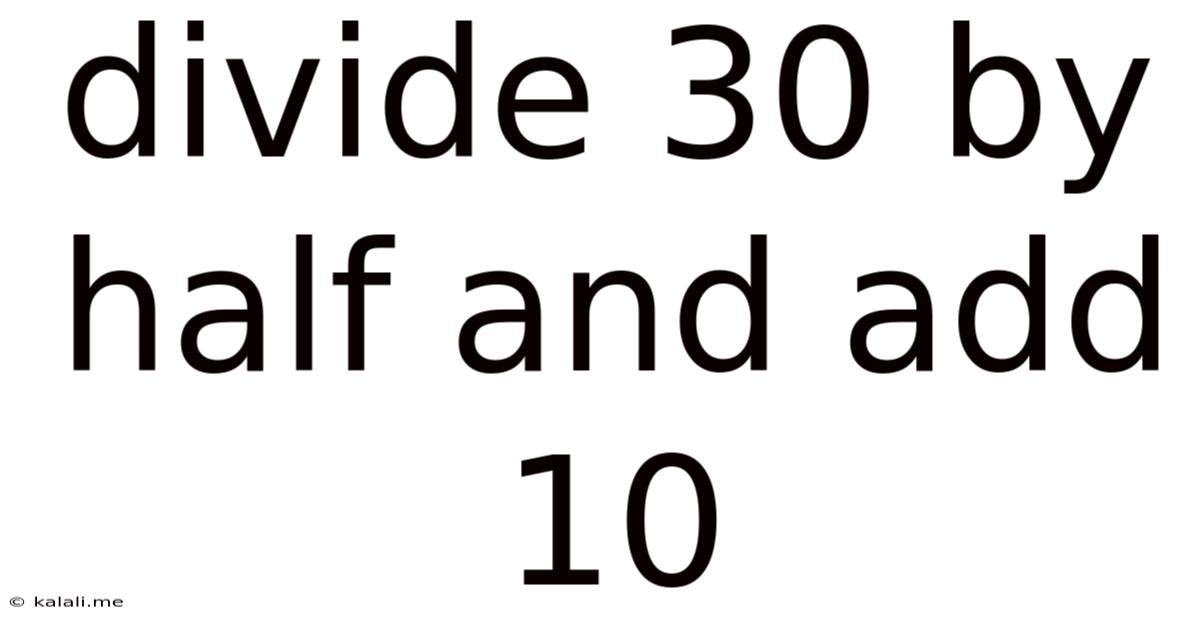
Table of Contents
Divide 30 by Half and Add 10: Unpacking a Simple Math Problem with Unexpected Depth
This seemingly simple math problem – "Divide 30 by half and add 10" – offers more than just a straightforward numerical answer. It's a perfect illustration of how easily ambiguity can creep into mathematical expressions and highlights the critical importance of precise language and order of operations. This article will delve into the problem, explore the different interpretations, and discuss the broader implications for clear communication in mathematics and beyond. We'll also touch upon how this seemingly simple problem can be used as a teaching tool to illustrate crucial mathematical concepts.
Understanding the Ambiguity: The Core of the Problem
The core issue lies in the phrase "divide 30 by half." Does this mean:
- Divide 30 by 1/2? This interpretation treats "half" as the fraction 1/2.
- Divide 30 by 2? This interpretation treats "half" as the number 2, representing one of two equal parts.
This ambiguity highlights the importance of precise mathematical notation. A more clearly written question might be: "Divide 30 by one-half, and then add 10" or "Divide 30 by 2, and then add 10." The difference in wording leads to drastically different answers.
Solving the Problem: Two Possible Interpretations
Let's examine both interpretations:
Interpretation 1: Dividing 30 by 1/2
This interpretation uses the fraction 1/2 to represent "half." Dividing by a fraction is equivalent to multiplying by its reciprocal. Therefore:
30 ÷ (1/2) = 30 × (2/1) = 60
Adding 10 to the result:
60 + 10 = 70
Therefore, under this interpretation, the answer is 70.
Interpretation 2: Dividing 30 by 2
This interpretation interprets "half" as the number 2. This is less common in formal mathematical contexts but is a perfectly valid interpretation given the ambiguity of the original phrasing. In this case:
30 ÷ 2 = 15
Adding 10 to the result:
15 + 10 = 25
Therefore, under this interpretation, the answer is 25.
The Importance of Order of Operations (PEMDAS/BODMAS)
While the ambiguity of "half" is the primary issue here, the order of operations also plays a role in ensuring a consistent and unambiguous solution. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) are mnemonic devices to remember the order. In this problem, the division is performed before the addition, regardless of the interpretation of "half".
Beyond the Numbers: Teaching Opportunities and Practical Applications
This seemingly simple problem provides several valuable teaching opportunities:
-
Ambiguity in Language: It emphasizes the importance of clear and precise language in mathematics. Students learn to appreciate the nuances of wording and how seemingly small changes can lead to significant differences in results. This extends beyond mathematics to other areas requiring precise communication, such as science, engineering, and programming.
-
Order of Operations: It reinforces the understanding of PEMDAS/BODMAS. Students solidify their understanding of the order in which operations must be performed to arrive at the correct answer. This is a fundamental concept in algebra and beyond.
-
Fractions and Reciprocals: The first interpretation provides a practical application of dividing by fractions and understanding the concept of reciprocals. It allows students to practice a crucial skill in arithmetic.
-
Problem-Solving Strategies: The problem encourages students to consider different interpretations and approaches to problem-solving. They develop critical thinking skills by analyzing potential ambiguities and justifying their chosen method.
-
Critical Reading Skills: The problem highlights the importance of carefully reading and understanding the question before attempting a solution. This develops crucial critical reading skills applicable in all academic disciplines.
Real-World Analogies and Extensions
The concept of ambiguity and precise wording isn't limited to mathematical expressions. Consider these real-world examples:
-
Recipe Instructions: Ambiguous instructions in a recipe can lead to disastrous results. Clear and precise language is essential.
-
Technical Manuals: Similarly, unclear instructions in a technical manual can lead to equipment malfunction or even injury.
-
Legal Documents: The precision of language in legal documents is paramount to avoid misinterpretations and legal disputes.
Addressing the Ambiguity: Writing Clear Mathematical Problems
To avoid the ambiguity present in the original problem, consider these strategies when writing mathematical problems:
- Use Fractions Explicitly: Instead of "half," write "1/2" or "one-half."
- Use Parentheses: Use parentheses to clearly indicate the order of operations. For example, "(30 ÷ (1/2)) + 10" removes any doubt about the intended calculation.
- Avoid Ambiguous Language: Opt for clear and precise wording that leaves no room for misinterpretation.
Conclusion: More Than Just Numbers
The seemingly simple problem of "Divide 30 by half and add 10" unveils a surprising depth. It's not just a matter of arriving at a numerical answer; it's a lesson in the importance of precise language, the order of operations, and the critical thinking skills needed to solve ambiguous problems. Understanding the different interpretations and their implications provides valuable insights into the nature of mathematical communication and its broader applications in the real world. This problem serves as a powerful reminder that clear communication is the cornerstone of effective problem-solving, not just in mathematics, but across all disciplines. By addressing the ambiguity and emphasizing precise language, we can ensure that mathematical problems are both solvable and conducive to deeper learning.
Latest Posts
Latest Posts
-
What Is A 2 Slope In Inches
Aug 20, 2025
-
I D Really Like To See You Tonight
Aug 20, 2025
-
If Someone Is 42 When Were They Born
Aug 20, 2025
-
Light Trucks Have High Center Of Gravity
Aug 20, 2025
-
Whats The Sand Color In Margarita Island
Aug 20, 2025
Related Post
Thank you for visiting our website which covers about Divide 30 By Half And Add 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.