Does A Triangle Have 3 Acute Angles
Kalali
Apr 04, 2025 · 5 min read
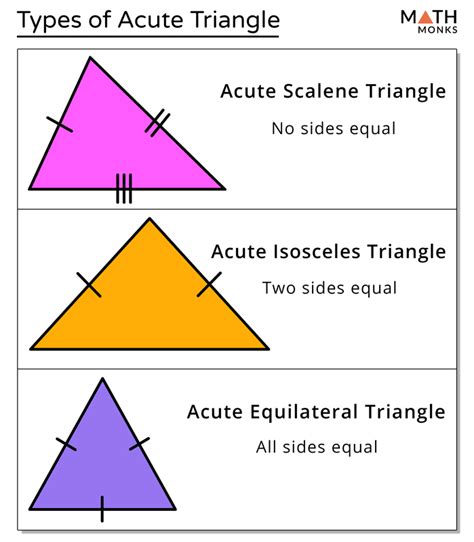
Table of Contents
Does a Triangle Have 3 Acute Angles? Exploring the Properties of Triangles
The question of whether a triangle can possess three acute angles is a fundamental concept in geometry. While seemingly straightforward, understanding this requires a deeper dive into the properties of triangles and their angle relationships. This article will explore this question comprehensively, examining different types of triangles, their angle properties, and the mathematical proofs that underpin our understanding. We'll delve into the limitations and exceptions, ultimately providing a clear and definitive answer while enhancing your understanding of triangle geometry.
Understanding Triangles and Their Angles
Before we address the central question, let's establish a solid foundation. A triangle is a closed two-dimensional geometric shape with three sides and three angles. The sum of the interior angles of any triangle always equals 180 degrees. This is a fundamental theorem in Euclidean geometry and forms the basis for numerous other geometric principles.
Types of Triangles Based on Angles:
Triangles are classified into several categories based on their angles:
- Acute Triangle: A triangle where all three angles are acute (less than 90 degrees).
- Right Triangle: A triangle with one right angle (exactly 90 degrees).
- Obtuse Triangle: A triangle with one obtuse angle (greater than 90 degrees).
The question we're addressing, "Does a triangle have 3 acute angles?", directly relates to the definition of an acute triangle.
Can a Triangle Have Three Acute Angles? The Answer and Proof
Yes, a triangle can have three acute angles. This type of triangle is called an acute triangle. However, it's crucial to understand the limitations and implications of this fact.
Let's consider a simple proof:
-
Start with the angle sum property: We know that the sum of the interior angles of any triangle is 180 degrees.
-
Assume three acute angles: Let's assume we have a triangle with three angles, A, B, and C, where each angle is less than 90 degrees (acute). Therefore: A < 90°, B < 90°, C < 90°.
-
Summation: If we add these angles together, we get A + B + C < 270°. This inequality highlights a crucial point: the sum of three acute angles is always less than 270°. Since the sum of angles in any triangle must be exactly 180°, there's room for three acute angles to exist without violating this fundamental property.
-
Illustrative Example: Imagine an equilateral triangle, where all three sides are equal in length. In an equilateral triangle, all three angles are equal, and since the total angle sum is 180°, each angle measures 60°. 60° is an acute angle, demonstrating a clear example of a triangle with three acute angles.
Exploring Other Triangle Types and Their Angle Relationships
While acute triangles exist, understanding the limitations imposed by the 180° angle sum rule helps us understand why triangles cannot have three obtuse angles or three right angles:
Why a Triangle Cannot Have Three Obtuse Angles:
If we assume a triangle has three obtuse angles (each greater than 90°), then the sum of those angles would be greater than 270°. This directly contradicts the fundamental theorem that the sum of angles in a triangle must equal 180°. Therefore, a triangle cannot have three obtuse angles.
Why a Triangle Cannot Have Three Right Angles:
Similarly, if a triangle had three right angles (each equal to 90°), the sum of those angles would be 270°. This also violates the 180° angle sum rule. Therefore, a triangle cannot have three right angles.
Right-Angled Triangles and Acute Angles:
In a right-angled triangle, one angle is 90°. The remaining two angles must be acute and add up to 90° to satisfy the 180° rule. This further reinforces the idea that acute angles are essential components within the broader framework of triangle geometry.
Practical Applications and Real-World Examples
Understanding the properties of triangles, especially the different types based on their angles, is crucial in various fields:
-
Engineering and Architecture: Structural stability in buildings, bridges, and other constructions heavily relies on understanding the angles and properties of triangles. Acute triangles often feature in designs due to their inherent stability.
-
Computer Graphics and Game Development: Triangle meshes are fundamental in 3D modeling and animation. The accurate calculation and manipulation of angles within these triangles are vital for realistic rendering and simulations.
-
Surveying and Navigation: Triangulation techniques used in surveying and GPS systems heavily utilize the properties of triangles to determine distances and locations accurately. The angles of the triangles formed by various points are crucial for these calculations.
-
Cartography and Mapmaking: Triangles are essential for representing geographical areas and creating accurate maps. The angles and side lengths of triangles are used to project three-dimensional surfaces onto two-dimensional maps.
Advanced Concepts and Further Exploration
The exploration of triangles extends far beyond the basics. More advanced concepts include:
-
Non-Euclidean Geometry: In geometries other than Euclidean geometry (e.g., spherical geometry), the angle sum property of triangles can differ. On a sphere, for example, the sum of angles in a triangle can be greater than 180°.
-
Trigonometry: Trigonometry deals with the relationships between angles and sides of triangles, providing a powerful mathematical framework for solving various problems involving triangles.
-
Vectors and Triangle Geometry: Vector methods can be used to elegantly represent and manipulate triangles and their properties.
Conclusion: The Definitive Answer
The answer to the question, "Does a triangle have 3 acute angles?", is a resounding yes, but only under specific circumstances. A triangle can have three acute angles, and such a triangle is classified as an acute triangle. However, it is important to remember the fundamental theorem that the sum of the interior angles of any triangle must equal 180 degrees. This constraint prevents triangles from having three obtuse angles or three right angles. Understanding this core principle, along with the various types of triangles and their properties, provides a firm foundation for further explorations in geometry and its vast applications. Acute triangles, with their unique characteristics and inherent stability, play a vital role in numerous fields, from engineering to computer graphics, emphasizing the importance of comprehending their fundamental properties.
Latest Posts
Latest Posts
-
How Many Cups Of Water Is 24 Oz
Apr 05, 2025
-
How Many Hours Is 95 Minutes
Apr 05, 2025
-
What Percentage Is 7 Of 12
Apr 05, 2025
-
How Many Oz Is 4 Pounds
Apr 05, 2025
-
106 Inches Is How Many Feet
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Does A Triangle Have 3 Acute Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
