Dominio Y Rango De Una Funcion
Kalali
Apr 03, 2025 · 7 min read
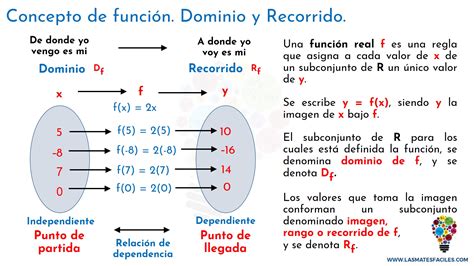
Table of Contents
Domain and Range of a Function: A Comprehensive Guide
Understanding the domain and range of a function is fundamental to mastering many concepts in algebra and calculus. This comprehensive guide will delve into the definitions, methods for finding them, and explore various examples to solidify your understanding. We’ll cover both theoretical aspects and practical applications, equipping you with the skills to confidently tackle domain and range problems.
What is the Domain of a Function?
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. In simpler terms, it's all the x-values you can "plug in" to the function and get a real, valid output. The domain is crucial because it defines the boundaries within which the function operates meaningfully. A function is undefined when its input leads to an undefined operation like division by zero or taking the square root of a negative number.
Identifying Potential Restrictions:
Several factors can restrict the domain of a function:
-
Division by Zero: Functions with denominators must exclude any values of x that make the denominator equal to zero. For example, in the function f(x) = 1/(x-2), the domain excludes x = 2 because it would result in division by zero.
-
Even Roots of Negative Numbers: Functions involving even roots (square roots, fourth roots, etc.) cannot have negative numbers under the radical sign. For example, in the function g(x) = √(x+3), the domain is restricted to x ≥ -3.
-
Logarithms: Logarithmic functions are only defined for positive arguments. For example, in the function h(x) = log(x), the domain is x > 0.
-
Specific Function Definitions: The definition of a function itself might explicitly limit the input values. For instance, a function might be defined only for integers or for a specific interval.
Finding the Domain: Step-by-Step Process
Let's break down the process of finding the domain of a function:
-
Identify Potential Problem Areas: Begin by examining the function to pinpoint any potential sources of restrictions, such as denominators, even roots, or logarithms.
-
Set up Inequalities or Equations: Based on the potential problem areas, formulate inequalities or equations to identify the values of x that lead to undefined operations.
-
Solve for x: Solve the inequalities or equations to find the values of x that must be excluded from the domain.
-
Express the Domain in Interval Notation or Set-Builder Notation: Express the domain using interval notation (e.g., (-∞, 2) ∪ (2, ∞)) or set-builder notation (e.g., {x | x ≠ 2}). Interval notation is generally preferred for its conciseness.
Examples of Finding the Domain:
Example 1: Find the domain of f(x) = (x+1) / (x² - 4).
-
Problem Areas: The denominator x² - 4 can be zero.
-
Equation: We set the denominator equal to zero: x² - 4 = 0.
-
Solving: Factoring gives (x-2)(x+2) = 0, so x = 2 or x = -2.
-
Domain: The domain is all real numbers except 2 and -2. In interval notation: (-∞, -2) ∪ (-2, 2) ∪ (2, ∞).
Example 2: Find the domain of g(x) = √(5-x).
-
Problem Areas: The expression under the square root must be non-negative.
-
Inequality: 5 - x ≥ 0
-
Solving: Solving for x gives x ≤ 5.
-
Domain: The domain is all real numbers less than or equal to 5. In interval notation: (-∞, 5].
Example 3: Find the domain of h(x) = log₂(2x - 6).
-
Problem Areas: The argument of the logarithm must be positive.
-
Inequality: 2x - 6 > 0
-
Solving: Solving for x gives x > 3.
-
Domain: The domain is all real numbers greater than 3. In interval notation: (3, ∞).
What is the Range of a Function?
The range of a function is the set of all possible output values (y-values) that the function can produce. It represents the complete set of values the function can achieve given its defined domain. Understanding the range is crucial for graphing and analyzing the behavior of the function.
Finding the Range: Methods and Techniques
Determining the range can be more challenging than finding the domain. Several methods are commonly used:
-
Graphing the Function: Graphing the function visually reveals the range as the set of all y-values covered by the graph. This method works well for simpler functions.
-
Algebraic Manipulation: This method involves solving for x in terms of y and then analyzing the resulting expression to determine the possible values of y.
-
Analyzing the Function's Behavior: Understanding the function's properties, like its increasing/decreasing intervals, asymptotes, and end behavior, can provide insights into its range.
-
Using the Inverse Function (if it exists): If a function has an inverse, the range of the original function is equal to the domain of its inverse.
Examples of Finding the Range:
Example 1: Find the range of f(x) = x².
-
Graphing: The graph of f(x) = x² is a parabola opening upwards. The y-values start at 0 and extend to infinity.
-
Algebraic: Since x² ≥ 0 for all real x, the range is [0, ∞).
Example 2: Find the range of g(x) = 1/(x+1).
-
Graphing: The graph is a hyperbola with a horizontal asymptote at y = 0 and a vertical asymptote at x = -1. The range is all real numbers except 0.
-
Algebraic: Let y = 1/(x+1). Then xy + y = 1, and xy = 1 - y. Solving for x gives x = (1-y)/y. This is undefined when y = 0. Therefore, the range is (-∞, 0) ∪ (0, ∞).
Example 3: Find the range of h(x) = √(x-2) + 1.
-
Graphing: The graph is a square root function shifted 2 units to the right and 1 unit up. The lowest y-value is 1, and it extends to infinity.
-
Algebraic: Since √(x-2) ≥ 0, the minimum value of h(x) is 1. The range is [1, ∞).
Domain and Range in Real-World Applications
Understanding domain and range is not just a theoretical exercise. It has crucial applications in various fields:
-
Physics: In physics, many formulas represent functions with restricted domains. For example, the formula for the period of a pendulum depends on the length of the pendulum, which must be positive.
-
Engineering: Engineers use functions to model systems and processes. The domain and range are vital for determining the operating limits and performance of these systems.
-
Economics: Economic models often involve functions relating variables like price and demand. The domain and range specify the feasible values of these variables.
-
Computer Science: In computer programming, understanding the domain and range of functions is essential for preventing errors and ensuring the program's stability. Input validation often involves checking if an input falls within the function's domain.
Advanced Concepts and Challenges
-
Piecewise Functions: Functions defined by different expressions over different intervals require careful consideration of each piece's domain and range to determine the overall domain and range.
-
Implicit Functions: Finding the domain and range of implicitly defined functions can be more challenging and might require advanced techniques like implicit differentiation.
-
Multivariable Functions: Functions with multiple independent variables (e.g., z = f(x, y)) have a domain that is a region in a plane and a range that is a set of real numbers.
Conclusion
Mastering the concepts of domain and range is a cornerstone of mathematical understanding. By systematically identifying potential restrictions, employing appropriate methods, and understanding the real-world implications, you can confidently analyze and work with functions across diverse fields. This guide has provided a comprehensive overview, equipping you with the knowledge and tools to tackle domain and range problems with accuracy and efficiency. Remember that practice is key; work through numerous examples to solidify your understanding and build your problem-solving skills.
Latest Posts
Latest Posts
-
How Many Eighths In A Quarter Pound
Jul 18, 2025
-
Can The Sine Of An Angle Ever Equal 2
Jul 18, 2025
-
How Many Months Is A Hundred Days
Jul 18, 2025
-
Mother And I Or Mother And Me
Jul 18, 2025
-
How Many Oz In One Water Bottle
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about Dominio Y Rango De Una Funcion . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.